题目内容
16.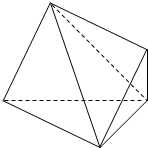 如图:已知正方形ABCD的边长为2,且AE⊥平面CDE,AD与平面CDE所成角为30°.
如图:已知正方形ABCD的边长为2,且AE⊥平面CDE,AD与平面CDE所成角为30°.(1)求证:AB∥平面CDE;
(2)求三棱锥D-ACE的体积.
分析 (1)通过AB∥CD,利用直线与平面平行的判定定理证明AB∥平面CDE.
(2)证明CD⊥平面ADE,CD⊥DE.通过体积转化VD-ACE=VA-CDE.求解即可.
解答 证明:(1)正方形ABCD中,AB∥CD,又AB?平面CDE,CD?平面CDE,
所以AB∥平面CDE.
(2)因为AE⊥平面CDE,AD与平面CDE所成角为30°∴∠ADE=30°∴AE=1
因为AE⊥平面CDE,且CD?平面CDE,所以AE⊥CD,
又正方形ABCD中,CD⊥AD,且AE∩AD=A,AE,AD?平面ADE,
所以CD⊥平面ADE,又DE?平面ADE,
所以CD⊥DE.
∵$CD=2,DE=\sqrt{3}$.
∴${V_{D-ACE}}={V_{A-CDE}}=\frac{1}{3}•\frac{1}{2}2•\sqrt{3}•1=\frac{{\sqrt{3}}}{3}$.
点评 本题考查几何体的体积的求法,直线与平面平行的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
11.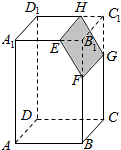 如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )
如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )
 如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )
如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )| A. | EH∥FG | B. | 四边形EFGH是矩形 | ||
| C. | Ω是棱柱 | D. | 四边形EFGH可能为梯形 |
5.下列命题中的说法正确的是( )
| A. | 若向量$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一的实数λ使得$\overrightarrow a=λ\overrightarrow b$ | |
| B. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| C. | 命题“?x0∈R,使得${x_0}^2+{x_0}+1<0$”的否定是:“?x∈R,均有x2+x+1≥0” | |
| D. | “a≠5且b≠-5”是“a+b≠0”的充分不必要条件 |