题目内容
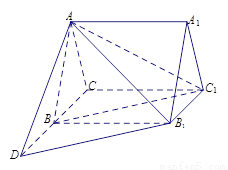
如图,正三棱柱![]() 的底面边长为
的底面边长为![]() ,侧棱长为
,侧棱长为![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
(1) 若![]() ,求证:直线
,求证:直线![]() 平面
平面![]() ;
;
(2)是否存在点![]() , 使平面
, 使平面![]() ⊥平面
⊥平面![]() ,若存在,请确定点
,若存在,请确定点![]() 的位置,若不存在,请说明理由;
的位置,若不存在,请说明理由;
(3)请指出点![]() 的位置,使二面角
的位置,使二面角![]() 平面角的大小为
平面角的大小为![]() .
.
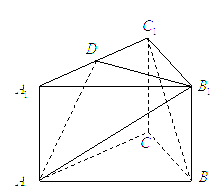
(1)略(2)不存在(3)点![]() 在棱
在棱![]() 上且
上且![]()
解析:
(1)证:连接![]() 交
交![]() 于
于![]() 点, ……(1分)
点, ……(1分)
在平行四边形![]() 中,
中,
有![]() ,又
,又![]() ……(2分)
……(2分)
∴![]() 为
为![]() 的中位线,从而
的中位线,从而![]() ,
,
又![]() 平面
平面![]() ∴直线
∴直线![]() 平面
平面![]() ; ……(3分)
; ……(3分)
(2)解:假设存在点![]() ,使平面
,使平面![]() ⊥平面
⊥平面![]() ,
,
过点![]() 作
作![]() 于
于![]() ,则
,则![]() 平面
平面![]() ,
,
又过![]() 作
作![]() 于
于![]() ,则
,则![]() 平面
平面![]() , ……(5分)
, ……(5分)
而过平面外一点有且仅有一条直线与已知平面垂直,故![]() 、
、![]() 应重合于
应重合于![]() 点,此时应有
点,此时应有![]() ,故
,故![]() ,
,
又点![]() 在棱
在棱![]() 上,故
上,故![]() ,
,
显然矛盾,故不存在这样的点![]() ,使平面
,使平面![]() ⊥平面
⊥平面![]() . ……(7分)
. ……(7分)

(3)解:连接![]() ,过
,过![]() 作
作![]() 于
于![]() .由(2)中的作法可知
.由(2)中的作法可知
![]() 为二面角
为二面角![]() 平面角, ……(8分)
平面角, ……(8分)
设![]() ,则
,则![]() ,
,
则可得![]() ,
,![]() ,
,
![]() , ……(10分)
, ……(10分)
∴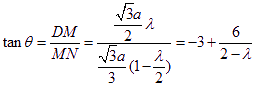 .∴
.∴![]()

练习册系列答案
相关题目
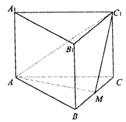
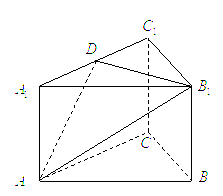
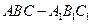 的底面边长为
的底面边长为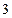
 ,侧棱
,侧棱 ,
,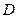 是
是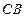 延长线上一点,且
延长线上一点,且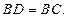
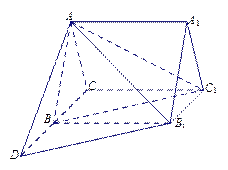
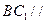 平面
平面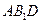 ;
;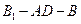 的大小.
的大小.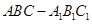 的底面边长为
的底面边长为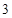 ,侧棱
,侧棱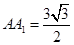 ,
, 是
是 延长线上一点,且
延长线上一点,且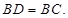
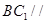 平面
平面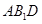 ;
;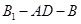 的大小.
的大小.