题目内容
(8分)已知函数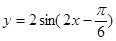 .
.
(1)写出它的振幅、周期、频率和初相;
(2)求这个函数的单调递减区间;
(3)求出使这个函数取得最大值时,自变量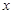 的取值集合,并写出最大值。
的取值集合,并写出最大值。
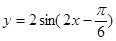 .
.(1)写出它的振幅、周期、频率和初相;
(2)求这个函数的单调递减区间;
(3)求出使这个函数取得最大值时,自变量
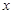 的取值集合,并写出最大值。
的取值集合,并写出最大值。(1)振幅2,周期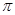 ,频率
,频率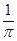 ,初相
,初相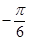 (2)
(2)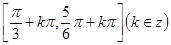
(3)当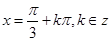 ,函数有最大值
,函数有最大值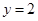
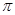 ,频率
,频率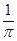 ,初相
,初相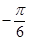 (2)
(2)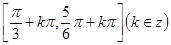
(3)当
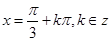 ,函数有最大值
,函数有最大值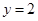
试题分析:(1)振幅2,周期
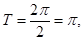 ,频率
,频率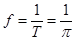 ,初相
,初相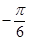 (2)令
(2)令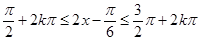 整理得
整理得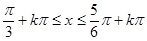 (3)函数最大值为2,此时需满足
(3)函数最大值为2,此时需满足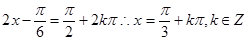
点评:三角函数
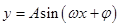 最值由振幅A决定,周期由
最值由振幅A决定,周期由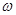 决定,平移由
决定,平移由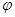 决定,求增区间令
决定,求增区间令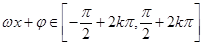 ,求减区间令
,求减区间令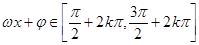 ,在高考题中已知条件常给出一个较复杂的三角函数式,需要考生利用诱导公式,和差角的正余弦公式,二倍角公式等将其化简为
,在高考题中已知条件常给出一个较复杂的三角函数式,需要考生利用诱导公式,和差角的正余弦公式,二倍角公式等将其化简为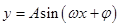 的形式
的形式
练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
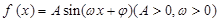 的图象如图所示,
的图象如图所示,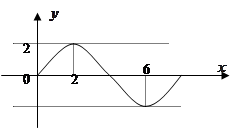
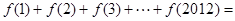 .
.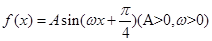 的最大值2,其图象相邻两条对称轴之间的距离为
的最大值2,其图象相邻两条对称轴之间的距离为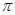 。
。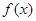 的解析式;
的解析式;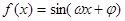 的图象(部分)如图所示,则
的图象(部分)如图所示,则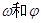 的取值是( )
的取值是( )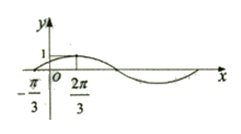
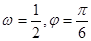

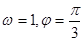
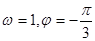
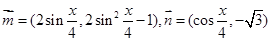 ,函数
,函数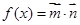 .
.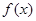 的最大值,并写出相应
的最大值,并写出相应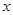 的取值集合;
的取值集合;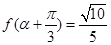 ,且
,且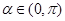 ,求
,求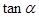 的值.
的值.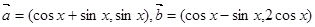 ,设
,设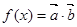 .
.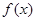 的最小正周期,并写出
的最小正周期,并写出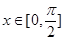 时,求函数
时,求函数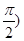 上为增函数且以
上为增函数且以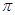 为周期的函数是
为周期的函数是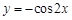
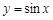
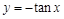
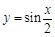
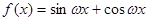 ,如果存在实数
,如果存在实数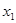 ,使得对任意的实数x,都有
,使得对任意的实数x,都有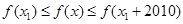 成立,则
成立,则 的最小值为 ( )
的最小值为 ( )



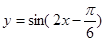 的图象,可以将函数
的图象,可以将函数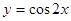 的图象向右平移 ______个单位长度
的图象向右平移 ______个单位长度