题目内容
11.求证:$\frac{1}{n+1}$(1+$\frac{1}{3}$+…+$\frac{1}{2n-1}$)$>\frac{1}{n}$($\frac{1}{2}+\frac{1}{4}$+…+$\frac{1}{2n}$)(n∈N,n≥2)分析 由$\frac{1}{2}≥$$\frac{1}{2}$>$\frac{1}{4}$>>$\frac{1}{6}$>…>$\frac{1}{2n}$,可得$\frac{n}{2}$>$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2n}$,则有$\frac{n}{2}$+$\frac{n}{12}$+$\frac{n}{30}$+…+$\frac{n}{2n•(2n-1)}$>$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2n}$,
而$\frac{1}{2n•(2n-1)}$=$\frac{1}{2n-1}$-$\frac{1}{2n}$,再由拆项和合并,即可得证.
解答 证明:由$\frac{1}{2}≥$$\frac{1}{2}$>$\frac{1}{4}$>>$\frac{1}{6}$>…>$\frac{1}{2n}$,
即有$\frac{n}{2}$>$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2n}$,
则有$\frac{n}{2}$+$\frac{n}{12}$+$\frac{n}{30}$+…+$\frac{n}{2n•(2n-1)}$>$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2n}$,
而$\frac{1}{2n•(2n-1)}$=$\frac{1}{2n-1}$-$\frac{1}{2n}$,
即有$\frac{n}{2}$+$\frac{n}{12}$+$\frac{n}{30}$+…+$\frac{n}{2n•(2n-1)}$=n(1-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{5}$-$\frac{1}{6}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n}$)
=n(1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2n-1}$)-n($\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{2n}$)>$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2n}$,
即n(1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2n-1}$)>(n+1)($\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2n}$),
也就是$\frac{1}{n+1}$(1+$\frac{1}{3}$+…+$\frac{1}{2n-1}$)$>\frac{1}{n}$($\frac{1}{2}+\frac{1}{4}$+…+$\frac{1}{2n}$).
点评 本题考查不等式的证明,主要考查放缩法证明不等式,注意运用不等式的性质,属于中档题.

| A. | a<b<c | B. | c<b<a | C. | b<a<c | D. | a<c<b |
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
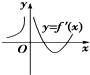
 设函数f(x)在定义域内可导且其图象如图①所示,则导函数y=f′(x)的图象最有可能是( )
设函数f(x)在定义域内可导且其图象如图①所示,则导函数y=f′(x)的图象最有可能是( )