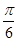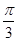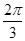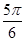题目内容
已知e1,e2是夹角为60°的两个单位向量,若a=e1+e2,b=-4e1+2e2,则a与b的夹角为( )
| A.30° | B.60° | C.120° | D.150° |
C
解析试题分析:由已知,是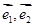 夹解角为
夹解角为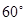 的两个单位向量,所以,
的两个单位向量,所以,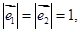
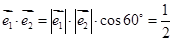 ,
,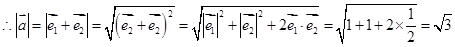

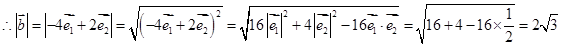
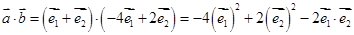 =
=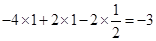
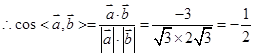 ,又因为
,又因为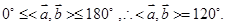 故选C.
故选C.
考点:1、向量的概念;2、向量的数量积;3、向量的夹角公式.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
给出下列结论:①若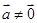 ,
,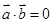 ,则
,则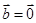 ; ②若
; ②若 ,则
,则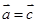 ;
;
③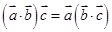 ; ④
; ④ ;⑤若
;⑤若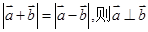
其中正确的为( )
| A.②③④ | B.①②⑤ | C.④⑤ | D.③④⑤ |
已知点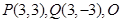 为坐标原点,动点
为坐标原点,动点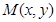 满足
满足 ,则点
,则点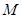 所构成的平面区域的面积是( )
所构成的平面区域的面积是( )
| A.12 | B.16 | C.32 | D.64 |
已知向量 ,
, .若
.若
 ,则实数
,则实数 的值为( )
的值为( )
A. | B. | C. | D. |
已知 是边长为
是边长为 的正三角形,
的正三角形,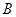 为线段
为线段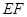 的中点,且
的中点,且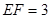 ,则
,则 的取值范围是( )
的取值范围是( )
A.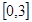 | B.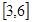 | C.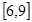 | D.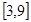 |
平面向量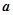 与
与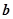 的夹角为60°,
的夹角为60°,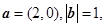 则
则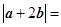 ( )
( )
A.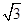 | B.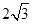 | C.4 | D.12 |
已知圆O(O为坐标原点)的半径为1,PA,PB为该圆的两条切线,A,B为两切点,那么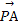 ·
·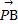 的最小值为( )
的最小值为( )
A.-4+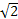 | B.-3+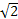 |
C.-4+2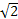 | D.-3+2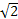 |
已知向量a=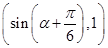 ,b=(4,4cos α-
,b=(4,4cos α- ),若a⊥b,则sin
),若a⊥b,则sin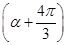 等于( )
等于( )
A.-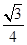 | B.-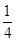 |
C.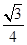 | D.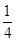 |