题目内容
10.若关于x的不等式ax-b>0的解集为(-∞,1),则关于x的不等式(ax+b)(x-2)>0的解为(-1,2).分析 根据不等式ax-b>0的解集得出a、b的关系,把不等式(ax+b)(x-2)>0化简并求出解集来.
解答 解:∵关于x的不等式ax-b>0的解集为(-∞,1),
∴a<0,且$\frac{b}{a}$=1;
∴关于x的不等式(ax+b)(x-2)>0
可化为(x+1)(x-2)<0,
解得-1<x<2,
∴不等式的解集为(-1.2)
答案为:(-1,2).
点评 本题考查了含有字母系数的不等式的解法与应用问题,解题时应考虑字母系数的取值情况,是基础题.

练习册系列答案
相关题目
1.已知f(x)在R为奇函数,f(1)=$\frac{1}{2}$,f(x+2)=f(x)+f(2),则f(6)=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | 3 |
2.已知a,b∈N*,f(x)=ex-2x,则“f(a)>f(b)”是“a>b”的 ( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必娄条件 |
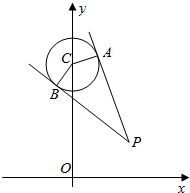 已知P(x0,y0)是圆C:x2+(y-4)2=1外一点,过P作圆C的切线,切点为A、B,记:四边形PACB的面积为f(P)
已知P(x0,y0)是圆C:x2+(y-4)2=1外一点,过P作圆C的切线,切点为A、B,记:四边形PACB的面积为f(P)