题目内容
利用独立性检验来考虑两个分类变量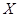
与
是否有关系时，通过查阅下表来确定“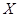和有关系”的可信度。如果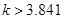
，那么就有把握认为“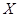和有关系”的百分比为（ ）
A．25% B．95% C．5% D．97.5%
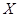与是否有关系时，通过查阅下表来确定“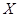和有关系”的可信度。如果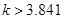，那么就有把握认为“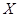和有关系”的百分比为（ ） |  |  |  |  |  |  |  |  |  |  |
 |  |  |  |  |  |  |  |  |  |  |
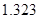B
试题分析：解：∵k＞5、024，
而在观测值表中对应于5.024的是0.025，
∴有1-0.025=97.5%的把握认为“X和Y有关系”，
故选D．.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
名年龄段在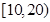
，
，
，
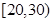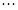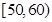的市民进行问卷调查，由此得到样本的频率分布直方图如图所示.
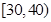的人数；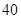 
岁的人中按年龄段分层抽样的方法随机抽取
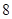人，求
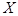为年龄在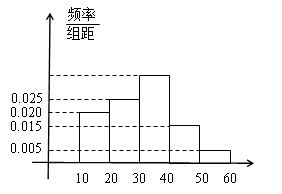
，由此请估计出山高为72（km）处气温的度数为（ ）
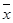＝101，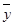
≈10.113 3，
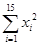＝161 125，
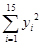＝1 628.55，
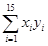＝16 076.8)