题目内容
11.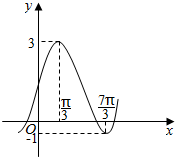 已知平面向量$\overrightarrow{a}$=(sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$,cos2$\frac{ωx}{2}$),$\overrightarrow{b}$=(cosφ,sinφ),函数f(x)=2A($\overrightarrow{a}$•$\overrightarrow{b}$)-Asinφ+k(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示.
已知平面向量$\overrightarrow{a}$=(sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$,cos2$\frac{ωx}{2}$),$\overrightarrow{b}$=(cosφ,sinφ),函数f(x)=2A($\overrightarrow{a}$•$\overrightarrow{b}$)-Asinφ+k(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示.(1)求函数f(x);
(2)如何由函数y=-sinx的图象得到函数y=f(x)的图象.
分析 (1)由条件利用两个向量的数量积公式,三角恒等变换,化简f(x)的解析式,由最大值和最小值求得k和A的值,由周期求出ω,由五点法作图求出φ的值,即可确定f(x)的解析式.
(2)由条件利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:(1)函数f(x)=2A($\overrightarrow{a}$•$\overrightarrow{b}$)-Asinφ+k=2A•[sin$\frac{ωx}{2}$cos$\frac{ωx}{2}$cosφ+cos2$\frac{ωx}{2}$sinφ]-Asinφ+k
=A•[sinωxcosφ+sinφ+sinφcosωx]-Asinφ+k=A[sin(ωx+φ)+sinφ]-Asinφ+k=Asin(ωx+φ)+k,
结合f(x)的图象可得k=$\frac{3-1}{2}$=1,故f(x)=Asin(ωx+φ)+1.
由$\frac{T}{2}$=$\frac{π}{ω}$=$\frac{7π}{3}$-$\frac{π}{3}$=2π,求得ω=$\frac{1}{2}$;再根据五点法作图可得$\frac{1}{2}$•$\frac{π}{3}$+φ=$\frac{π}{2}$,A=$\frac{3-(-1)}{2}$=2,
求得φ=$\frac{π}{3}$,故f(x)=2sin($\frac{1}{2}$x+$\frac{π}{3}$)+1.
(2)把函数y=-sinx=sin(x+π)的图象上点的横坐标变为原来的2倍,得到y=sin($\frac{1}{2}$x+π)的图象;
再把所得图象向右平移$\frac{4π}{3}$个单位,可得y=sin[$\frac{1}{2}$(x-$\frac{4π}{3}$)+π]=sin($\frac{1}{2}$x+$\frac{π}{3}$)的图象;
再把所得图象的点的纵坐标变为原来的2倍,得到y=2sin($\frac{1}{2}$x+$\frac{π}{3}$)的图象;
再把所得图象向上平移1个单位,可得f(x)=2sin($\frac{1}{2}$x+$\frac{π}{3}$)+1的图象.
点评 本题主要考查两个向量的数量积公式,三角恒等变换,由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的图象变换规律,属于中档题.

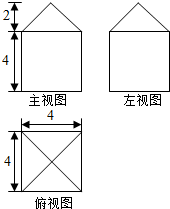
| A. | (80+16$\sqrt{2}$)cm2 | B. | 96cm2 | C. | (96+16$\sqrt{2}$)cm2 | D. | 112cm2 |
| A. | (-∞,-$\frac{{e}^{2}+1}{e}$) | B. | (-∞,e2) | C. | (-2e2,1-e2) | D. | (1-e2,1) |