题目内容
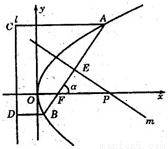
 倾斜角为α的直线经过抛物线y2=8x的焦点F,且与抛物线交于A,B两点.
倾斜角为α的直线经过抛物线y2=8x的焦点F,且与抛物线交于A,B两点.(1)若|AF|,4,|BF|成等差数列,求直线AB的方程;
(2)若α为锐角,作线段AB的垂直平分线m交于x轴于点P,试证明|FP|-|FP|cos2α为定值,并求此定值.
分析:(1)解1:由|AF|,4,|BF|成等差数列,知|AF|+|BF|=8=|AB|.由y2=8x,知焦点F为(2,0).设AB的方程为:x=my+2,得y2-8my-16=0,由韦达定理和弦长公式能求出直线AB方程.
解2:令A(x1•y1),B(x2•y2),则|AF|=x1+2|BF|=x2+2,所以线段AB的中点的横标为
=2.直线AB过焦点F(2,0),由此能求出直线AB方程.
(2)由已知令直线AB的方程为y=tanα•(x-2),由
得:x2tam2α-4(tan2α+2)x+4tan2α=0∴x1+x2=
y1+y2=tanα•(x1+x2-4)=
=
,所以AB中线m的方程为:y-
=-
(x-
),由此能够证明|FP|-|FP|cos2α为定值,并能求出此定值.
解2:令A(x1•y1),B(x2•y2),则|AF|=x1+2|BF|=x2+2,所以线段AB的中点的横标为
| x1+x2 |
| 2 |
(2)由已知令直线AB的方程为y=tanα•(x-2),由
|
| 4(tan2α+2) |
| tanα |
| 8tanα |
| tan2α |
| 8 |
| tanα |
| 4 |
| tanα |
| 1 |
| tanα |
| 2tan2α+4 |
| tan2α |
解答:(1)解法一:∵|AF|,4,|BF|成等差
∴|AF|+|BF|=8=|AB|
∵y2=8x
∴焦点F为(2,0)
设AB的方程为:x=my+2
则由:
⇒y2=8(my+2)
得 y2-8my-16=0
∴y1+y2=8m,y1•y2=-16
∴弦长|AB|=
•|y1-y2|
=
•
=
•
=8(1+m2)=8
∴m=0
∴直线AB方程为x=2.
解法二:令A(x1•y1),B(x2•y2),
则|AF|=x1+2,|BF|=x2+2
∴|AF|+|BF|=x1+x2+4=8
即x1+x2=4
∴线段AB的中点的横标为
=2
而直线AB过焦点F(2,0),
∴直线AB垂直x轴
即AB方程为x=2.
(2)证明:由已知令直线AB的方程为y=tanα•(x-2),则
由
得:
∴x2tanα-4(tan2α+2)x+4tan2α=0,
∴x1+x2=
y1+y2=tanα•(x1+x2-4)=
=
∴AB的中点为(
,
).
∴AB中垂线m的方程为:y-
=-
(x-
)
令 y=0得:x=6+
∴|PF|=|x-2|=4+
∴|PF|-|PF|•cos2α=|PF|(1-cos2α)=2|PF|•sin2α
=8(1+
)•sin2α=8×(1+
)•sin2α
=8.
∴|AF|+|BF|=8=|AB|
∵y2=8x
∴焦点F为(2,0)
设AB的方程为:x=my+2
则由:
|
得 y2-8my-16=0
∴y1+y2=8m,y1•y2=-16
∴弦长|AB|=
| 1+m2 |
=
| 1+m2 |
| (y1+y2)2-4y1y2 |
=
| 1+m2 |
| 64m2+64 |
∴m=0
∴直线AB方程为x=2.
解法二:令A(x1•y1),B(x2•y2),
则|AF|=x1+2,|BF|=x2+2
∴|AF|+|BF|=x1+x2+4=8
即x1+x2=4
∴线段AB的中点的横标为
| x1+x2 |
| 2 |
而直线AB过焦点F(2,0),
∴直线AB垂直x轴
即AB方程为x=2.
(2)证明:由已知令直线AB的方程为y=tanα•(x-2),则
由
|
∴x2tanα-4(tan2α+2)x+4tan2α=0,
∴x1+x2=
| 4(tan2α+2) |
| tanα |
| 8tanα |
| tan2α |
| 8 |
| tanα |
∴AB的中点为(
| 2(tan2α+2) |
| tan2α |
| 4 |
| tanα |
∴AB中垂线m的方程为:y-
| 4 |
| tanα |
| 1 |
| tanα |
| 2tan2α+4 |
| tan2α |
令 y=0得:x=6+
| 4 |
| tan2α |
∴|PF|=|x-2|=4+
| 4 |
| tan2α |
∴|PF|-|PF|•cos2α=|PF|(1-cos2α)=2|PF|•sin2α
=8(1+
| 1 |
| tan2α |
| cos2α |
| sin2α |
=8.
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,难度大,容易出错.解题时要认真审题,注意韦达定理和弦长公式的灵活运用.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知倾斜角为45°的直线经过A(2,4),B(1,m)两点,则m=( )
| A、3 | B、-3 | C、5 | D、-1 |
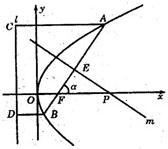 如图,倾斜角为a的直线经过抛物线y2=8x的焦点F,且于抛物线交于A、B两点.
如图,倾斜角为a的直线经过抛物线y2=8x的焦点F,且于抛物线交于A、B两点.