题目内容
如图，半径为2的⊙O中，∠AOB=90°，D为OB的中点，AD的延长线交⊙O于点E，则线段DE的长为
- A.
- B.
- C.
- D.
C
分析：延长BO交⊙O与点C，我们根据已知中⊙O的半径为2，，∠AOB=90°，D为OB的中点，我们易得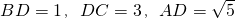
，代入相交弦定理，我们即可求出线段DE的长．
解答：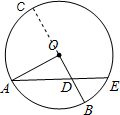
解：延长BO交⊙O与点C，
由题设知：，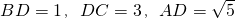
又由相交弦定理知AD•DE=BD•DC，
得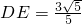
故选C
点评：本题考查的知识是与圆有关的比例线段，其中延长B0交圆于另一点C，从而构造相交弦的模型是解答本题的关键．
分析：延长BO交⊙O与点C，我们根据已知中⊙O的半径为2，，∠AOB=90°，D为OB的中点，我们易得
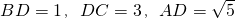，代入相交弦定理，我们即可求出线段DE的长．解答：
解：延长BO交⊙O与点C，由题设知：
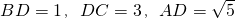，又由相交弦定理知AD•DE=BD•DC，
得
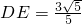
故选C
点评：本题考查的知识是与圆有关的比例线段，其中延长B0交圆于另一点C，从而构造相交弦的模型是解答本题的关键．
练习册系列答案
相关题目
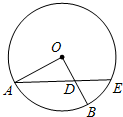（几何证明选讲选做题）如图，半径为2的⊙O中，∠AOB=90°，D为OB的中点，AD的延长线交⊙O于点E，则线段DE的长为
如图，半径为2的⊙O中，∠AOB=90°，D为OB的中点，AD的延长线交⊙O于点E，则线段DE的长为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
，
为
的中点，
的延长线交⊙O于点
，则线段
的长为_______.
，
为
的中点，
的延长线交⊙O于点
，则线段
的长为_______.