题目内容
【题目】如图,在平面直角坐标系中,点A![]() ,B
,B![]() ,锐角α的终边与单位圆O交于点P.
,锐角α的终边与单位圆O交于点P.
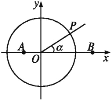
(1)用α的三角函数表示点P的坐标;
(2)当![]() =-
=-![]() 时,求α的值;
时,求α的值;
(3)在x轴上是否存在定点M,使得|![]() |=
|=![]() |恒成立?若存在,求出点M的坐标;若不存在,请说明理由.
|恒成立?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)(cos α,sin α);(2)α=60°;(3)M(-2,0).
【解析】
![]() 用
用![]() 的三角函数的坐标法定义得到答案
的三角函数的坐标法定义得到答案
![]() 首先写出两个向量的坐标,根据
首先写出两个向量的坐标,根据![]() ,整理计算即可求出
,整理计算即可求出![]() 的值
的值
![]() 假设存在定点
假设存在定点![]() ,进行向量的模长运算,求得恒成立时的
,进行向量的模长运算,求得恒成立时的![]() 值
值
(1)用α的三角函数表示点P的坐标为(cos α,sin α).
(2)![]() ,
,
![]() =-
=-![]() 时,
时,
即![]() +sin2α=-
+sin2α=-![]() ,
,
整理得到cos α=![]() ,所以锐角α=60°.
,所以锐角α=60°.
(3)在x轴上假设存在定点M,设M(x,0),![]() =(cos α-x,sin α),
=(cos α-x,sin α),
则由|![]() |=
|=![]() |恒成立,得到
|恒成立,得到![]() +cos α=
+cos α=![]() (1-2xcos α+x2),整理得2(2+x)cos α=x2-4,
(1-2xcos α+x2),整理得2(2+x)cos α=x2-4,
当x=-2时等式恒成立,所以存在M(-2,0).

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目