题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
解:y= |
(2) |
解:∵f(x)= |

练习册系列答案
相关题目
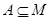 ,集合A中所有元素的乘积称为集合A
,集合A中所有元素的乘积称为集合A