题目内容
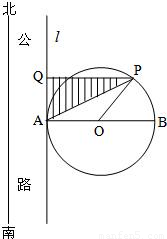
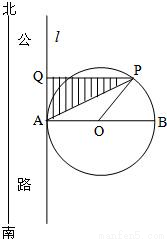
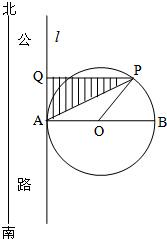 如图,在南北方向有一条公路,一半径为100m的圆形广场(圆心为O)与此公路一边所在直线l相切于点A.点P为北半圆弧(弧APB)上的一点,过P作直线l的垂线,垂足为Q.计划在△PAQ内(图中阴影部分)进行绿化.设△PAQ的面积为S(单位:m2).
如图,在南北方向有一条公路,一半径为100m的圆形广场(圆心为O)与此公路一边所在直线l相切于点A.点P为北半圆弧(弧APB)上的一点,过P作直线l的垂线,垂足为Q.计划在△PAQ内(图中阴影部分)进行绿化.设△PAQ的面积为S(单位:m2).(1)设∠BOP=α(rad),将S表示为α的函数;
(2)确定点P的位置,使绿化面积最大,并求出最大面积.
分析:(1)若∠BOP=α,则P点坐标(x,y)中,x=AQ=100sinα,y=PQ=100+100cosα,α∈(0,π),根据三角形面积公式,我们易将S表示为α的函数.
(2)由(1)中结论,我们可利用导数法,判断函数的单调性,进而求出函数的最大值,即最大绿化面积.
(2)由(1)中结论,我们可利用导数法,判断函数的单调性,进而求出函数的最大值,即最大绿化面积.
解答:解:(1)AQ=100sinα,PQ=100+100cosα,α∈(0,π),
则△PAQ的面积S=
AQ•PQ=
×100sinα×(100+100cosα)
=5000(sinα+sinαcosα),(0<α<π).
(2)S/=5000(cosα+cos2α-sin2α)
=5000(2cos2α+cosα-1)
=5000(2cosα-1)(cosα+1),
令S/=0,得cosα=
,cosα=-1(舍去),此时α=
.
当0<α<
时,
<cosα<1,S/>0,S关于α为增函数;
当
<α<π时,-1<cosα<
,S/<0,S关于α为减函数.
∴当α=
时,Smax=3750
(m2),此时PQ=150m.
答:当点P距公路边界l为150m时,绿化面积最大,Smax=3750
m2.
则△PAQ的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
=5000(sinα+sinαcosα),(0<α<π).
(2)S/=5000(cosα+cos2α-sin2α)
=5000(2cos2α+cosα-1)
=5000(2cosα-1)(cosα+1),
令S/=0,得cosα=
| 1 |
| 2 |
| π |
| 3 |
当0<α<
| π |
| 3 |
| 1 |
| 2 |
当
| π |
| 3 |
| 1 |
| 2 |
∴当α=
| π |
| 3 |
| 3 |
答:当点P距公路边界l为150m时,绿化面积最大,Smax=3750
| 3 |
点评:本题考查的知识点是在实际问题中建立三角函数的模型,及利用导数计算,闭区间上函数的最值.在构造函数时,一定要根据P为北半圆弧(弧APB)上的一点,限制0<α<π,这是本题中易忽略的点.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
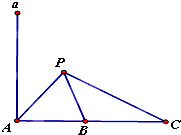 如图,a是海面上一条南北方向的海防警戒线,在a上一点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20km和54km处.某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A,20s后监测点C相继收到这一信号.在当时的气象条件下,声波在水中的传播速度是1.5km/s.
如图,a是海面上一条南北方向的海防警戒线,在a上一点A处有一个水声监测点,另两个监测点B,C分别在A的正东方20km和54km处.某时刻,监测点B收到发自静止目标P的一个声波,8s后监测点A,20s后监测点C相继收到这一信号.在当时的气象条件下,声波在水中的传播速度是1.5km/s.