题目内容
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的轴的正半轴重合.直线的参数方程是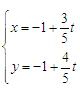 (为参数),曲线C的极坐标方程为
(为参数),曲线C的极坐标方程为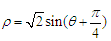 .
.
(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)设直线与曲线C相交于M,N两点,求M,N两点间的距离.
(Ⅰ)x2+y2-x-y=0;(Ⅱ)
解析试题分析:(Ⅰ)利用x= ,y=
,y= ,
,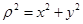 可把曲线C的极坐标方程转化为直角坐标方程.(Ⅱ)把直线l的参数方程转化为普通方程,求出圆心到直线l的距离,最后利用勾股定理即可求出MN的长度.
可把曲线C的极坐标方程转化为直角坐标方程.(Ⅱ)把直线l的参数方程转化为普通方程,求出圆心到直线l的距离,最后利用勾股定理即可求出MN的长度.
试题解析:(Ⅰ)将曲线C的极坐标方程化为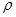 =
=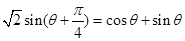 ,所以
,所以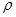 2=
2= ,
,
即x2+y2=x+y,所以曲线C的直角坐标方程x2+y2-x-y="0."
(Ⅱ)直线l的参数方程中消去参数t可得普通方程4x-3t+1=0,而圆的普通方程为x2+y2-x-y=0,所以圆心C( ,
, ),半径r=
),半径r=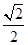 ,圆心C到直线l的距离d=
,圆心C到直线l的距离d= 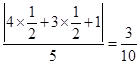 ,
,
所以直线l被圆C截得的弦长为: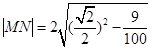 =
= .即M、N两点间的距离为
.即M、N两点间的距离为 .
.
考点:1.极坐标方程、参数方程、普通方程以及它们之间的互化;2.点到直线的距离公式.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 (ρ∈R). (2)ρcos2
(ρ∈R). (2)ρcos2 =1.
=1. ,以
,以 为极点,
为极点,  轴的非负半轴为极轴建立极坐标系,
轴的非负半轴为极轴建立极坐标系, 点的极坐标为
点的极坐标为 ,曲线
,曲线 的极坐标方程为
的极坐标方程为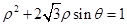
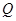 为曲线
为曲线 中点
中点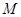 到直线
到直线 (
(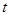 为参数)距离的最小值.
为参数)距离的最小值. 过点P(-2,-4)的直线
过点P(-2,-4)的直线 为参数)与曲线C相交于点M,N两点.
为参数)与曲线C相交于点M,N两点. 的普通方程;
的普通方程; 被直线
被直线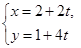 (
(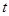 是参数)截得的弦长.
是参数)截得的弦长. 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系. 的极坐标方程是
的极坐标方程是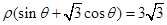 ,射线
,射线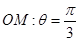 与圆C的交点为O,P,与直线
与圆C的交点为O,P,与直线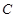 的圆心
的圆心 ,半径
,半径
 ,直线
,直线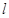 的参数方程为
的参数方程为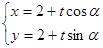 (
( 为参数),直线
为参数),直线 两点,求弦长
两点,求弦长 的取值范围
的取值范围 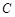 的极坐标方程是
的极坐标方程是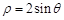 ,直线的参数方程是
,直线的参数方程是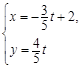 (为参数).
(为参数).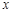 轴的交点是
轴的交点是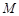 ,
,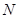 是曲线
是曲线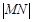 的最大值.
的最大值.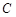 经过点
经过点 ,圆心为直线
,圆心为直线 与极轴的交点,求圆
与极轴的交点,求圆