题目内容
(文)将n2个正整数1,2,3,…n2填入n×n个方格中,使得每行、每列、每条对角线上的数的和相等,这个正方形就叫做n阶幻方,如图就是一个3 阶幻方,定义f(n)为n阶幻方对角线上数的和,例如f(3)=15,则f(4)=| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
【答案】分析:欲求4阶幻方对角线上数之和,只需求每一行上数之和,由n阶幻方定义可知,4阶幻方由1到42,共16个连续自然数构成,且每一行都相等,所以,只需求出所有数之和,再除以4即可得答案.
解答:解:由等差数列得前n项和公式可得,所有数之和S=1+2+3+…+42=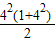 =136,所以,f(4)=
=136,所以,f(4)=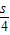 =
=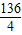 =34
=34
故答案为:34.
点评:本题考查等差数列的前n项和公式,题型新颖,解题时要认真分析,仔细解答,避免错误.
解答:解:由等差数列得前n项和公式可得,所有数之和S=1+2+3+…+42=
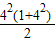 =136,所以,f(4)=
=136,所以,f(4)=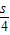 =
=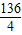 =34
=34 故答案为:34.
点评:本题考查等差数列的前n项和公式,题型新颖,解题时要认真分析,仔细解答,避免错误.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目