题目内容
14.长方体ABCD-A1B1C1D1中,E、F分别为线段AA1、B1C上的点,若AB=6,BC=5.AA1=3.则三棱锥D1-EDF的体积为( )| A. | $\frac{15}{2}$ | B. | 15 | ||
| C. | 30 | D. | 随点E、F的改变而改变的值 |
分析 因为B1C∥平面EDD1,所以三棱锥D1-EDF的体积等于三棱锥F-EDD1,的体积,棱锥的高为长方体的棱长CD,底面EDD1,是以3为底5为高的三角形,利用棱锥的体积公式可求.
解答 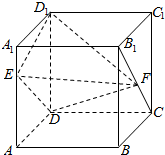 解:∵B1C∥平面EDD1,
解:∵B1C∥平面EDD1,
∴三棱锥D1-EDF的体积等于三棱锥F-EDD1的体积,而三棱锥F-EDD1,底面EDD1,是以3为底5为高的三角形,三棱锥F-EDD1的高为6,
∴V=$\frac{1}{3}×\frac{1}{2}×3×5×6$=15
故选B.
点评 本题考查了棱锥的体积,关键是明确三棱锥D1-EDF的体积等于三棱锥F-EDD1的体积,进一步明确其底面面积和高,利用体积公式解答.

练习册系列答案
相关题目
6.若三点A(0,a,2b),B(2,3,4),C(3,4,5)共线,则下列等式成立的是( )
| A. | 2a=b | B. | a+b=2 | C. | 2a-b=3 | D. | a-2b=1 |
3.若非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,满足$\overrightarrow{a}$•$\overrightarrow{b}$=0,且|$\overrightarrow{a}$-$\overrightarrow{b}$|=2|$\overrightarrow{a}$|,则向量$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
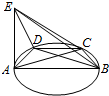 已知三棱锥E-ABD各个面均为直角三角形,且Rt△ADE的直角顶点为A,其中AE=AB,∠ABD=$\frac{π}{6}$,以AB为直径在平面ABD内画圆,且经过点D,任取圆上一点C(不与A,B两点重合).
已知三棱锥E-ABD各个面均为直角三角形,且Rt△ADE的直角顶点为A,其中AE=AB,∠ABD=$\frac{π}{6}$,以AB为直径在平面ABD内画圆,且经过点D,任取圆上一点C(不与A,B两点重合).