Question

(本题满分12分)（学选修4-4的选做题1，没学的选做题2）
题1：已知点M是椭圆C:+ ＝1上的任意一点,直线l:x+2y-10＝0.
(1)设x＝3cosφ,φ为参数,求椭圆C的参数方程；
(2)求点M到直线l距离的最大值与最小值.
题2：函数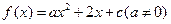的一个零点是１，另一个零点在（－1,0）内，（1）求的取值范围；
（2）求出的最大值或最小值，并用表示．

Answer 1

解： (1)把x＝3cosφ代入+ ＝1,得到+ ＝1,
于是y²＝4(1-cos²φ)＝4sin²φ,
即y＝±2 sinφ.                                ……………………2分
由参数φ的任意性,可取y＝2 sinφ.
因此,椭圆C的参数方程是             ………………………4分
(2)设点M(3cosφ,2sinφ),由点到直线的距离公式,得到点M到直线l的距离为
d＝＝,
其中θ满足sinθ＝,cosθ＝.                ……………………………10分
∴sin(φ+θ)＝-1时，点M到直线l距离取最大值3；
sin(φ+θ)＝1时，点M到直线l距离取最小值.  ……………………12分

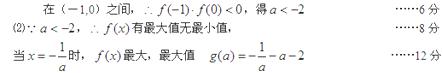
解析