题目内容
已知函数![]()
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)是否存在实数![]() ,对任意的
,对任意的![]() ,且
,且![]() ,有
,有![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
解:(1)![]()
![]()
①当![]() 时,
时,![]() ,由
,由![]() 得
得![]() ,
,![]() 得
得![]()
②当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,由
,由![]() 得
得![]() ;
;
③当![]() 时,
时,![]() 恒成立;
恒成立;
④当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,由
,由![]() 得
得![]() ;
;
综上,当![]() 时,
时,![]() 在
在![]() 单调递减;在
单调递减;在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 和
和![]() 上单调递增;在
上单调递增;在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在
在![]() 和
和![]() 上单调递增;在
上单调递增;在![]() 上单调递减
上单调递减
(2)∵![]() ,∴
,∴![]() ,
,![]()
令![]()
![]()
要使![]() ,只要
,只要![]() 在
在![]() 上为增函数,即
上为增函数,即![]() 在
在![]() 上恒成立,
上恒成立,
因此![]() ,即
,即![]()
故存在实数![]() ,对任意的
,对任意的![]() ,且
,且![]() ,有
,有![]() 恒成立
恒成立

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
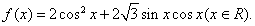
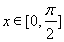
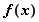

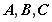
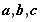
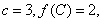
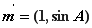
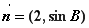
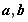

 时,求函数的最大值和最小值;
时,求函数的最大值和最小值; 的取值范围,使
的取值范围,使 在区间
在区间 上是单调减函数
上是单调减函数 .(
.( ).
). 时,求函数
时,求函数 的极值;
的极值; (2)若对
(2)若对 ,有成立,求实数
,有成立,求实数 的取值范围.
的取值范围.
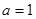 时,求
时,求 的极小值;
的极小值; ,求
,求 的最大值
的最大值 .
.