题目内容
复平面上,非零复数z1,z2在以i为圆心,1为半径的圆上,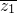 z2的实部为零,z1的辐角主值为
z2的实部为零,z1的辐角主值为 ,则z2=________.
,则z2=________.
- +
+ i
i
分析:利用已知条件求出复数z1的辐角主值,复数z1共轭复数的三角形式与z2的三角形式,通过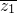 z2的实部为零,求出复数z2.
z2的实部为零,求出复数z2.
解答:z1满足|z-i|=1;argz1= ,得z1=
,得z1= +
+ i,
i,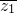 =cos(-
=cos(- )+isin(-
)+isin(- ).
).
设z2的辐角为θ(0<θ<π),则z2=2sinθ(cosθ+isinθ).
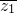 •z2=2sinθ[cos(θ-
•z2=2sinθ[cos(θ- )+isin(θ-
)+isin(θ- )],
)],
若其实部为0,则θ- =
= ,于是θ=
,于是θ= .
.
z2=- +
+ i.
i.
故答案为:- +
+ i.
i.
点评:本题考查复数的代数形式与三角形式的互化,复数的辐角主值,复数的分类,考查计算能力.
 +
+ i
i分析:利用已知条件求出复数z1的辐角主值,复数z1共轭复数的三角形式与z2的三角形式,通过
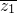 z2的实部为零,求出复数z2.
z2的实部为零,求出复数z2.解答:z1满足|z-i|=1;argz1=
 ,得z1=
,得z1= +
+ i,
i,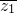 =cos(-
=cos(- )+isin(-
)+isin(- ).
).设z2的辐角为θ(0<θ<π),则z2=2sinθ(cosθ+isinθ).
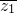 •z2=2sinθ[cos(θ-
•z2=2sinθ[cos(θ- )+isin(θ-
)+isin(θ- )],
)],若其实部为0,则θ-
 =
= ,于是θ=
,于是θ= .
.z2=-
 +
+ i.
i.故答案为:-
 +
+ i.
i.点评:本题考查复数的代数形式与三角形式的互化,复数的辐角主值,复数的分类,考查计算能力.

练习册系列答案
相关题目
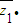 z2的实部为零,z1的辐角主值为
z2的实部为零,z1的辐角主值为 ,则z2= .
,则z2= .