题目内容
(07年四川卷理)(12分)已知函数![]() ,设曲线
,设曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴的交点为
轴的交点为![]()
![]() ,其中
,其中![]() 为正实数.
为正实数.
(Ⅰ)用![]() 表示
表示![]() ;
;
(Ⅱ) 证明:对一切正整数![]() 的充要条件是
的充要条件是![]()
(Ⅲ)若![]() ,记
,记![]() ,证明数列
,证明数列![]() 成等比数列,并求数列
成等比数列,并求数列![]() 的通项公式。
的通项公式。
本题综合考察数列、函数、不等式、导数应用等知识,以及推理论证、计算及解决问题的能力。
解析:(Ⅰ)由题可得![]()
所以过曲线上点![]() 的切线方程为
的切线方程为![]() ,
,
即![]()
令![]() ,得
,得![]() ,即
,即![]()
显然![]() ∴
∴![]()
(Ⅱ)证明:(必要性)
若对一切正整数![]() ,则
,则![]() ,即
,即![]() ,而
,而![]() ,∴
,∴![]() ,即有
,即有![]()
(充分性)若![]() ,由
,由![]()
用数学归纳法易得![]() ,从而
,从而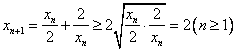 ,即
,即![]()
又![]() ∴
∴![]()
于是![]()
![]() ,
,
即![]() 对一切正整数
对一切正整数![]() 成立
成立
(Ⅲ)由![]() ,知
,知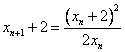 ,同理,
,同理,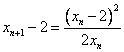
故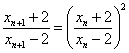
从而![]() ,即
,即![]()
所以,数列![]() 成等比数列,故
成等比数列,故![]() ,
,
即![]() ,从而
,从而![]()
所以![]()

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目