题目内容
设x=1与x=2是f(x)=alnx+bx2+x函数的两个极值点.(1)试确定常数a和b的值;
(2)试判断x=1,x=2是函数f(x)的极大值点还是极小值点,并求相应极值.
分析:(1)函数的极值点处的导数值为0,列出方程,求出a,b的值.
(2)由(1)作出表示x,f′(x),f(x)的关系的表格;据极值的定义,求出极值.
(2)由(1)作出表示x,f′(x),f(x)的关系的表格;据极值的定义,求出极值.
解答:解:(1)f′(x)=
+2bx+1,
由已知得:
?
,
∴
(2)x变化时.f′(x),f(x)的变化情况如表:
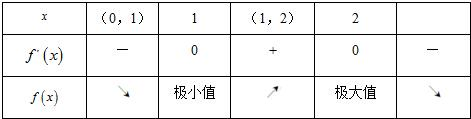
故在x=1处,函数f(x)取极小值
;在x=2处,函数f(x)取得极大值
-
ln2
| a |
| x |
由已知得:
|
|
∴
|
(2)x变化时.f′(x),f(x)的变化情况如表:

故在x=1处,函数f(x)取极小值
| 5 |
| 6 |
| 4 |
| 3 |
| 2 |
| 3 |
点评:本题考查函数的极值点的导数的值为0、利用 导数求函数的单调性、极值.

练习册系列答案
相关题目