题目内容
关于平面向量的命题①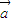 •
•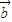 =
=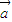 •
• 且
且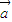 ≠
≠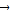 时,必有
时,必有 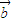 =
=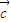 ②如
②如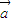 ∥
∥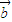 时,必存在唯一实数λ使
时,必存在唯一实数λ使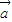 =λ
=λ ③
③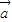 ,
,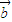 ,
,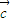 互不共线时,
互不共线时,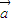 -
-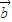 必与
必与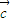 不共线④
不共线④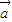 与
与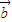 共线且
共线且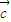 与
与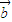 也共线时,则
也共线时,则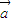 与
与 必共线其中正确命题个数有( )
必共线其中正确命题个数有( )A.0个
B.1个
C.2个
D.3个
【答案】分析:举出反例即可否定一个命题,本题所给的四个命题皆可举出反例,从而选出答案.
解答:解:①当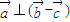 ,且
,且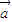 ≠
≠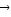 时,则满足
时,则满足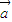 •
•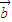 =
=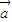 •
•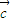 ,但是未必有
,但是未必有 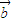 =
=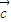 ,故①不正确.
,故①不正确.
②当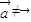 ,
,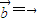 时,虽然满足条件
时,虽然满足条件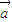 ∥
∥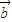 ,但是不存在实数λ使
,但是不存在实数λ使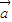 =λ
=λ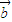 ,故②不正确.
,故②不正确.
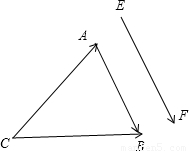
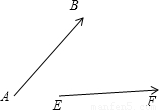
③如图所示,AB∥EF,设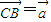 ,
,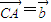 ,则
,则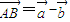 ,满足
,满足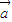 -
-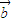 与
与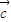 共线,故③不正确.
共线,故③不正确.
④取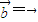 ,设
,设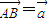 ,
,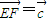 ,则满足
,则满足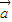 与
与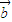 共线且
共线且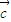 与
与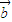 也共线,则
也共线,则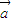 与
与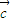 未必共线.
未必共线.
故④不正确.
综上可知,正确命题个数为0.
故选A.
点评:本题考查了向量的共线和垂直,充分理解向量的共线定理和数量积是解决问题的关键.
解答:解:①当
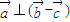 ,且
,且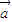 ≠
≠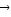 时,则满足
时,则满足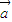 •
•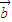 =
=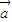 •
•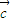 ,但是未必有
,但是未必有 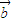 =
=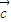 ,故①不正确.
,故①不正确.②当
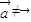 ,
,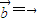 时,虽然满足条件
时,虽然满足条件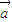 ∥
∥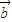 ,但是不存在实数λ使
,但是不存在实数λ使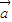 =λ
=λ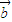 ,故②不正确.
,故②不正确.③如图所示,AB∥EF,设
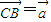 ,
,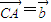 ,则
,则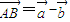 ,满足
,满足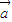 -
-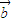 与
与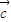 共线,故③不正确.
共线,故③不正确.
④取
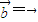 ,设
,设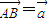 ,
,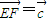 ,则满足
,则满足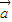 与
与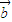 共线且
共线且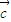 与
与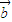 也共线,则
也共线,则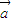 与
与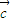 未必共线.
未必共线.
故④不正确.
综上可知,正确命题个数为0.
故选A.
点评:本题考查了向量的共线和垂直,充分理解向量的共线定理和数量积是解决问题的关键.

练习册系列答案
相关题目
 •
• =
= 且
且 时,必有
时,必有 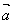 ·
·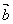 =
=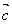 且
且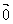 时,必有
时,必有
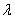 使
使
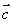 不共线;④
不共线;④