Question

在区间[1、2]上，若f（x）=x²+2ax是减函数而g（x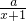）=是增函数，则a的取值范围是

1. A.
   （-2，1）∪（1，2）
2. B.
   （-∞，-2]
3. C.
   [-2，0）
4. D.
   [2，+∞]

Answer 1

B
分析：利用二次函数的性质可得[1，2]⊆（-∞，-a]，从而可求；结合反比例函数的单调性进一步可求A得取值范围
解答：∵f（x）=x²+2ax=（x+a）²-a²的递减区间为（-∞，-a]
又∵在区间[1，2]上单调递减
∴[1，2]⊆（-∞，-a]
∴-a≥2即a≤-2
∵在区间{1，2]上单调递增
∴a＜0
∴a≤-2
故选：B
点评：本题主要考查了二次函数与反比例函数的单调性的应用，解题得关键是要能够寻求已知函数的单调区间，进而求解参数的范围．