题目内容
(本题满分12分)已知抛物线的顶点在原点,对称轴是x轴,抛物线上的点M(-3,m)到焦点的距离为5,求抛物线的方程和m的值.
y2=-8x,m=±2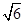
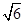
试题分析:法一:根据已知条件,抛物线方程可设为y2=-2px(p>0),…………3分
则焦点F(-
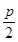 ,0).…………5分
,0).…………5分∵点M(-3,m)在抛物线上,且|MF|=5,…………8分
故
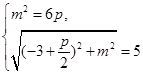 ,解得
,解得 ,…………11分
,…………11分∴抛物线方程为y2=-8x,m=±2
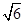 .…………12分
.…………12分法二:设抛物线方程为y2=-2px(p>0),则准线方程为x=
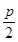 ,…………3分
,…………3分由抛物线定义,M点到焦点的距离等于M点到准线的距离,…………5分
∴有
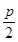 -(-3)=5,∴p=4.…………8分
-(-3)=5,∴p=4.…………8分∴所求抛物线方程为y2=-8x,…………10分
又∵点M(-3,m)在抛物线上,故m2=(-8)×(-3),∴m=±2
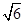 .…………12分
.…………12分点评:本题利用抛物线定义求解比较简单

练习册系列答案
相关题目
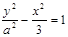 的焦点为F1,F2.离心率为2。
的焦点为F1,F2.离心率为2。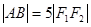 ,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。
,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。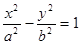 的离心率
的离心率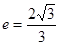 ,过
,过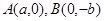 的直线到原点的距离是
的直线到原点的距离是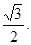
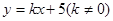 交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值. 分别是双曲线
分别是双曲线 的左、右焦点,P为双曲线右支上一点,I是
的左、右焦点,P为双曲线右支上一点,I是 的内心,且
的内心,且 ,则
,则 = _________.
= _________.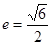 的是( )
的是( )



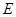 的中心在原点
的中心在原点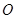 ,焦点
,焦点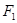 ,
,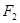 在
在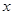 轴上,经过点
轴上,经过点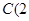 ,
,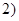 ,且抛物线
,且抛物线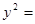
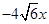 的焦点为
的焦点为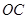 的直线
的直线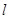 与椭圆
与椭圆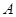 ,
,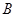 两点,当以
两点,当以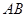 为直径的圆
为直径的圆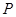 与
与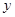 轴相切时,求直线
轴相切时,求直线 的左焦点
的左焦点 ,
, 为坐标原点,点
为坐标原点,点 在椭圆上,点
在椭圆上,点 在椭圆的右准线上,若
在椭圆的右准线上,若 ,则椭圆的离心率为 .
,则椭圆的离心率为 .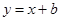 与曲线
与曲线 有公共点,则
有公共点,则 的取值范围是 .
的取值范围是 .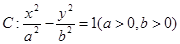 的离心率为
的离心率为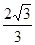 ,且过点P(
,且过点P(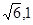 ).
).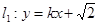 与双曲线C恒有两个不同的交点A,B,且
与双曲线C恒有两个不同的交点A,B,且