题目内容
已知函数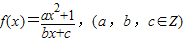 是奇函数,f(-1)=-2,f(2)<3.
是奇函数,f(-1)=-2,f(2)<3.(1)求函数f(x)解析式;
(2)若g(x)=x•f(x),ϕ(x)=g[g(x)]-λg(x),试问:是否存在实数λ,使∅(x)在(-∞,-1)内是单调递减,在(-1,0)内是单调递增的,若存在,求λ值;若不存在,说明理由.
(3)附加题:若
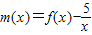 ,研究函数m(x),写出m(x)性质,并画出图象.
,研究函数m(x),写出m(x)性质,并画出图象.
【答案】分析:(1)由题意可得f(-x)=-f(x),即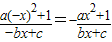 可求c,再由f(-1)=-2,f(2)<3结合a,b∈Z 可求a,b,进而可求f(x)
可求c,再由f(-1)=-2,f(2)<3结合a,b∈Z 可求a,b,进而可求f(x)
(2)由(1)可得g(x)=xf(x)=1+x2,则∅(x)=g[g(x)]-λg(x)=x4+(2-λ)x2+2-λ,对函数求导可得∅′(x)=4x3+2(2-λ)x,若使函数∅(x)在(-∞,-1)内是单调递减,在(-1,0)内是单调递增,则∅;(-1)=0即-4-2(2-λ)=0,可求λ,代入检验是否符合题意
(3)m(x)=f(x)-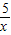 =
=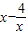 ,从函数的定义域、值域、单调性、奇偶性等方面研究函数的性质
,从函数的定义域、值域、单调性、奇偶性等方面研究函数的性质
解答:解:(1)∵函数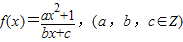 是奇函数,
是奇函数,
∴f(-x)=-f(x)
即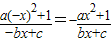
∴c=0,f(x)=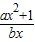
∵f(-1)=-2,f(2)<3.
∴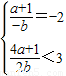
∵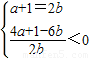
∴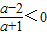 ,解得-1<a<2
,解得-1<a<2
∵a∈Z
∴a=0或a=1
当a=0时,b=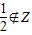
当a=1时,b=1,满足题意,此时f(x)=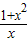
(2)∵g(x)=xf(x)=1+x2,
∅(x)=g[g(x)]-λg(x)=g(1+x2)-λ(1+x2)=1+(1+x2)2-λ(1+x2)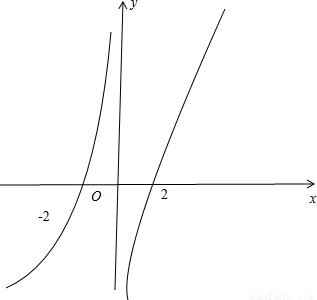
=x4+(2-λ)x2+2-λ
∴∅′(x)=4x3+2(2-λ)x
若使函数∅(x)在(-∞,-1)内是单调递减,在(-1,0)内是单调递增
则∅;(-1)=0即-4-2(2-λ)=0
∴λ=4,此时∅(x)=x4-2x2-2,∅′(x)=4x3-4x=4x(x-1)(x+1)
∅′(x)>0可得x>1或-1<x<0,即函数在(1,+∞),(-1,0)单调递增
∅′(x)<0可得0<x<1或x<-1即函数在(0,1),(-∞,-1)单调递减
使∅(x)在(-∞,-1)内是单调递减,在(-1,0)内是单调递增的λ=4
(3)m(x)=f(x)-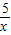 =
=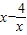 ,图象如右
,图象如右
定义域:(-∞,0)∪(0,+∞)
值域:R
奇偶性:m(-x)=-x+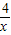 =-m(x),函数为奇函数
=-m(x),函数为奇函数
单调性:在(-∞,0),(0,+∞)上单调递增
点评:本题综合考查了函数的奇偶性的应用,利用导数判断函数的单调区间的存在及函数性质的研究,考查了考试探索新问题的能力
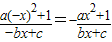 可求c,再由f(-1)=-2,f(2)<3结合a,b∈Z 可求a,b,进而可求f(x)
可求c,再由f(-1)=-2,f(2)<3结合a,b∈Z 可求a,b,进而可求f(x)(2)由(1)可得g(x)=xf(x)=1+x2,则∅(x)=g[g(x)]-λg(x)=x4+(2-λ)x2+2-λ,对函数求导可得∅′(x)=4x3+2(2-λ)x,若使函数∅(x)在(-∞,-1)内是单调递减,在(-1,0)内是单调递增,则∅;(-1)=0即-4-2(2-λ)=0,可求λ,代入检验是否符合题意
(3)m(x)=f(x)-
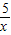 =
=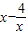 ,从函数的定义域、值域、单调性、奇偶性等方面研究函数的性质
,从函数的定义域、值域、单调性、奇偶性等方面研究函数的性质解答:解:(1)∵函数
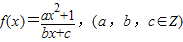 是奇函数,
是奇函数,∴f(-x)=-f(x)
即
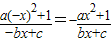
∴c=0,f(x)=
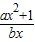
∵f(-1)=-2,f(2)<3.
∴
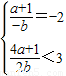
∵
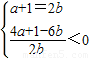
∴
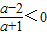 ,解得-1<a<2
,解得-1<a<2∵a∈Z
∴a=0或a=1
当a=0时,b=
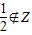
当a=1时,b=1,满足题意,此时f(x)=
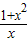
(2)∵g(x)=xf(x)=1+x2,
∅(x)=g[g(x)]-λg(x)=g(1+x2)-λ(1+x2)=1+(1+x2)2-λ(1+x2)

=x4+(2-λ)x2+2-λ
∴∅′(x)=4x3+2(2-λ)x
若使函数∅(x)在(-∞,-1)内是单调递减,在(-1,0)内是单调递增
则∅;(-1)=0即-4-2(2-λ)=0
∴λ=4,此时∅(x)=x4-2x2-2,∅′(x)=4x3-4x=4x(x-1)(x+1)
∅′(x)>0可得x>1或-1<x<0,即函数在(1,+∞),(-1,0)单调递增
∅′(x)<0可得0<x<1或x<-1即函数在(0,1),(-∞,-1)单调递减
使∅(x)在(-∞,-1)内是单调递减,在(-1,0)内是单调递增的λ=4
(3)m(x)=f(x)-
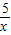 =
=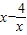 ,图象如右
,图象如右定义域:(-∞,0)∪(0,+∞)
值域:R
奇偶性:m(-x)=-x+
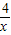 =-m(x),函数为奇函数
=-m(x),函数为奇函数单调性:在(-∞,0),(0,+∞)上单调递增
点评:本题综合考查了函数的奇偶性的应用,利用导数判断函数的单调区间的存在及函数性质的研究,考查了考试探索新问题的能力

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值.
是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值. 是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值.
是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值.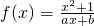 是奇函数且f(1)=2.(1)求a,b的值;(2)用定义判断f(x)在(-∞,-1)上的单调性.
是奇函数且f(1)=2.(1)求a,b的值;(2)用定义判断f(x)在(-∞,-1)上的单调性. 是奇函数,f(x)=lg(10x+1)+mx是偶函数.
是奇函数,f(x)=lg(10x+1)+mx是偶函数. ,若g(x)>h[lg(2a+1)]对任意x≥1恒成立,求实数a的取值范围.
,若g(x)>h[lg(2a+1)]对任意x≥1恒成立,求实数a的取值范围. (a>0),有下列四个命题:
(a>0),有下列四个命题: