题目内容
已知函数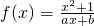 是奇函数且f(1)=2.(1)求a,b的值;(2)用定义判断f(x)在(-∞,-1)上的单调性.
是奇函数且f(1)=2.(1)求a,b的值;(2)用定义判断f(x)在(-∞,-1)上的单调性.
解:(1)因为f(-x)=-f(x)即
所以-ax+b=-ax-b∴b=0,又f(1)=2,所以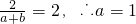
(2)由(1)得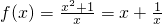
设x1,x2是(-∞,-1)上的任意两实数,且x1<x2,则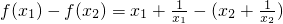 =
=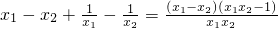 ,因为x1<x2<-1,所以x1-x2<0,x1x2>1,x1x2-1>0,所以f(x1)-f(x2)<0,f(x1)<f(x2)
,因为x1<x2<-1,所以x1-x2<0,x1x2>1,x1x2-1>0,所以f(x1)-f(x2)<0,f(x1)<f(x2)
所以f(x)在(-∞,-1)上是增函数.
分析:(1)由函数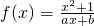 是奇函数得f(-x)=-f(x)即
是奇函数得f(-x)=-f(x)即 恒成立,化简得b=0,再由f(1)=2,可求得a值.
恒成立,化简得b=0,再由f(1)=2,可求得a值.
(2)由(1)得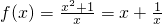 ,设x1,x2是(-∞,-1)上的任意两实数,且x1<x2,作差f(x1)-f(x2),将差化简为几个因子的乘积,再判断差的符号,用定义判断出结论.注意用定义法证明时的步骤.
,设x1,x2是(-∞,-1)上的任意两实数,且x1<x2,作差f(x1)-f(x2),将差化简为几个因子的乘积,再判断差的符号,用定义判断出结论.注意用定义法证明时的步骤.
点评:本题考点是函数的性质,主要考查函数奇偶性与单调性,是函数性质中的一道常规题型,是近几年高中教学中考查函数性质时常用的模式.

所以-ax+b=-ax-b∴b=0,又f(1)=2,所以
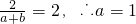
(2)由(1)得
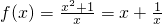
设x1,x2是(-∞,-1)上的任意两实数,且x1<x2,则
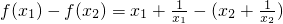 =
=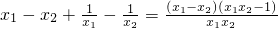 ,因为x1<x2<-1,所以x1-x2<0,x1x2>1,x1x2-1>0,所以f(x1)-f(x2)<0,f(x1)<f(x2)
,因为x1<x2<-1,所以x1-x2<0,x1x2>1,x1x2-1>0,所以f(x1)-f(x2)<0,f(x1)<f(x2)所以f(x)在(-∞,-1)上是增函数.
分析:(1)由函数
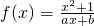 是奇函数得f(-x)=-f(x)即
是奇函数得f(-x)=-f(x)即 恒成立,化简得b=0,再由f(1)=2,可求得a值.
恒成立,化简得b=0,再由f(1)=2,可求得a值.(2)由(1)得
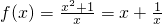 ,设x1,x2是(-∞,-1)上的任意两实数,且x1<x2,作差f(x1)-f(x2),将差化简为几个因子的乘积,再判断差的符号,用定义判断出结论.注意用定义法证明时的步骤.
,设x1,x2是(-∞,-1)上的任意两实数,且x1<x2,作差f(x1)-f(x2),将差化简为几个因子的乘积,再判断差的符号,用定义判断出结论.注意用定义法证明时的步骤.点评:本题考点是函数的性质,主要考查函数奇偶性与单调性,是函数性质中的一道常规题型,是近几年高中教学中考查函数性质时常用的模式.

练习册系列答案
相关题目
 是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值.
是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值. 是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值.
是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值.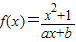 是奇函数且f(1)=2.(1)求a,b的值;(2)用定义判断f(x)在(-∞,-1)上的单调性.
是奇函数且f(1)=2.(1)求a,b的值;(2)用定义判断f(x)在(-∞,-1)上的单调性.