Question

设f（x）=min{2x+3，x²+1，11-3x}，则maxf（x）的值为

 

．

Answer 1

分析：根据函数f（x）的几何意义画出它的图象，数形结合可得maxf（x）的值．

解答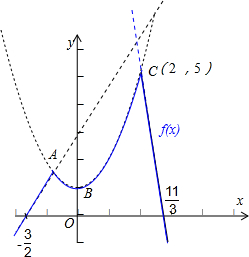：解：函数f（x）表示函数y=3x+3、y=x²+1、y=3-11x中的最小者，
它的图象如图所示：即图中蓝线部分，
显然，函数f（x）在点C处取得最大值为y_C，
由

y=11-3x y=x2+1

 可得

x=2 y=5

，就点C（2，5），
故maxf（x）=5，
故答案为 5．

点评：本题主要考查函数的最值的几何意义，体现了数形结合的数学而思想，属于中档题．