题目内容
设函数![]() ,其中
,其中![]() .
.
证明:当![]() 时,函数
时,函数![]() 没有极值点;当
没有极值点;当![]() 时,函数
时,函数![]() 有且只有一个极值点,并求出极值.
有且只有一个极值点,并求出极值.
证明:因为![]() ,所以
,所以![]() 的定义域为
的定义域为![]() .
.
![]()
![]() .
.
当![]() 时,如果
时,如果![]() 在
在![]() 上单调递增;
上单调递增;
如果![]() 在
在![]() 上单调递减.
上单调递减.
所以当![]() ,函数
,函数![]() 没有极值点.
没有极值点.
当![]() 时,
时,

令![]() ,
,
将![]() (舍去),
(舍去),![]() ,
,
当![]() 时,
时,![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
| 0 |
|
|
| 极小值 |
从上表可看出,
函数![]() 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为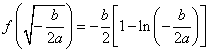 .
.
当![]() 时,
时,![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
| 0 |
|
|
| 极大值 |
从上表可看出,
函数![]() 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为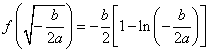 .
.
综上所述,
当![]() 时,函数
时,函数![]() 没有极值点;
没有极值点;
当![]() 时,
时,
若![]() 时,函数
时,函数![]() 有且只有一个极小值点,极小值为
有且只有一个极小值点,极小值为![]() .
.
若![]() 时,函数
时,函数![]() 有且只有一个极大值点,极大值为
有且只有一个极大值点,极大值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
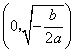
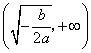
 ,其中
,其中 .证明:当
.证明:当 时,函数
时,函数 没有极值点;当
没有极值点;当 时,函数
时,函数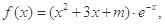 (其中
(其中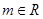 ,
,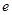 是自然对数的底数)
是自然对数的底数)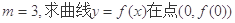 处的切线方程;
处的切线方程; 上有两个极值点.
上有两个极值点.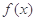 的极小值大于e.
的极小值大于e. ,其中
,其中 .
. 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性; ,不等式
,不等式 都成立.
都成立.