题目内容
设点F1,F2分别是椭圆C:
+
=1(a>b>0)的左、右焦点,P为椭圆C上任意一点,且
?
的最小值为0,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:先设点P(x,y),表示出
•
,然后消去y,得到关于x的二次函数,再根据二次函数的性质可得最值,从而得到a,b,c的等量关系,求出离心率.
| PF1 |
| PF2 |
解答:解:设点P(x,y)为椭圆C上任意一点,则
+
=1,
∴y2=b2(1-
),
∴
•
=(x+c,y)(x-c,y)=x2+y2-c2=x2+b2(1-
)-c2=(1-
)x2+b2-c2≥b2-c2,
∵
•
的最小值为0,
∴b2-c2=0,
则a2=b2+c2=2c2,
∴
=
=e2
即e=
.
故选:B.
| x2 |
| a2 |
| y2 |
| b2 |
∴y2=b2(1-
| x2 |
| a2 |
∴
| PF1 |
| PF2 |
| x2 |
| a2 |
| b2 |
| a2 |
∵
| PF1 |
| PF2 |
∴b2-c2=0,
则a2=b2+c2=2c2,
∴
| c2 |
| a2 |
| 1 |
| 2 |
即e=
| ||
| 2 |
故选:B.
点评:本题主要考查了椭圆的简单性质,以及向量数量积的应用和二次函数的最值,同时考查了分析问题的能力,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
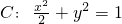 的左、右焦点,P为椭圆C上任意一点.
的左、右焦点,P为椭圆C上任意一点. 的取值范围;
的取值范围; 的左、右焦点,P为椭圆C上任意一点.
的左、右焦点,P为椭圆C上任意一点.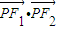 的取值范围;
的取值范围;