题目内容
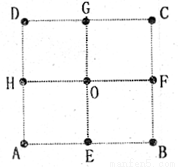如图，在正方形ABCD中，E、F、G、H是各边中点，O是正方形中心，在A、E、B、F、C、G、D、H、O这九个点中，以其中三个点为顶点作三角形，在这些三角形中，互不全等的三角形共有（ ）A．6个
B．7个
C．8个
D．9个
【答案】分析：由题意知题目条件比较特殊，相同位置的元素具有共同的性质，以A为顶点列举出所有可能的三角形有AEG，AEF，AEC，AEH，ABC，ABG，AFG；以E为顶点的有EHF，根据分类计数原理得到结果．
解答：解：在正方形ABCD中，E、F、G、H是各边中点，O是正方形中心，
题目条件比较特殊，相同位置的元素具有共同的性质，
以A为顶点列举出所有可能的三角形
有AEG，AEF，AEC，AEH，ABC，ABG，AFG
以E为顶点的有EHF
根据分类计数原理知共有7+1=8
故选C．
点评：排列组合问题在几何中的应用，在计算时要求做到，兼顾所有的条件，注意实际问题本身的限制条件，按元素的性质分类是处理带限制条件的组合问题的常用方法．
解答：解：在正方形ABCD中，E、F、G、H是各边中点，O是正方形中心，
题目条件比较特殊，相同位置的元素具有共同的性质，
以A为顶点列举出所有可能的三角形
有AEG，AEF，AEC，AEH，ABC，ABG，AFG
以E为顶点的有EHF
根据分类计数原理知共有7+1=8
故选C．
点评：排列组合问题在几何中的应用，在计算时要求做到，兼顾所有的条件，注意实际问题本身的限制条件，按元素的性质分类是处理带限制条件的组合问题的常用方法．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
如图，在多面体ABC-A1B1C1中，四边形A1ABB1是正方形，AB=AC，
（2012•青岛二模）如图，在多面体ABC-A1B1C1中，四边形ABB1A1是正方形，AC=AB=1，A1C=A1B，B1C1∥BC，
（2012•郑州二模）如图，在多面体ABC-A1B1C1中，四边形A1ABB1是正方形，AB=AC，BC=
BC．
BC．