题目内容
某大学2009届入学测试中,要求每位考生在10道题中随机抽出2道题回答.(I) 现在某位考生会答10道题中的6道,求这个考生答错题目个数的分布列和数学期望;
(II)若答对其中一题即为及格,如果某位考生及格的概率小于
 ,那么他最多会几道题?
,那么他最多会几道题?
【答案】分析:(1)答错题目的个数ξ=0,1,2,然后根据等可能事件的概率公式求出相应的概率,列出分布列,最后根据数学期望公式求出所求;
(2)设该考生会x道题,不会10-x道题,然后根据某位考生及格的概率小于 建立不等式,解之即可求出所求.
建立不等式,解之即可求出所求.
解答:解:(1)答错题目的个数ξ=0,1,2
P(ξ=0)=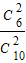 =
= ,P(ξ=1)=
,P(ξ=1)=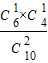 =
=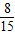 ,P(ξ=2)=
,P(ξ=2)=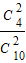 =
=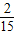
∴分布列为:
期望Eξ=0× +1×
+1×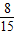 +2×
+2×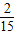 =
= (道题)…(7分)
(道题)…(7分)
(2)设该考生会x道题,不会10-x道题,则1-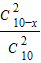 <
<
∴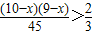 …(10分)
…(10分)
解得:x<4或x>15(舍),故该考生最多会3道题…(13分)
点评:本题主要考查了等可能事件的概率,以及离散型随机变量及其分布列和数学期望,同时考查了计算能力,属于中档题.
(2)设该考生会x道题,不会10-x道题,然后根据某位考生及格的概率小于
 建立不等式,解之即可求出所求.
建立不等式,解之即可求出所求.解答:解:(1)答错题目的个数ξ=0,1,2
P(ξ=0)=
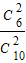 =
= ,P(ξ=1)=
,P(ξ=1)=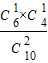 =
=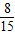 ,P(ξ=2)=
,P(ξ=2)=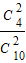 =
=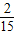
∴分布列为:
| ξ | 0 | 1 | 2 |
| P |  | 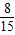 | 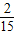 |
 +1×
+1×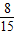 +2×
+2×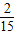 =
= (道题)…(7分)
(道题)…(7分)(2)设该考生会x道题,不会10-x道题,则1-
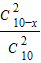 <
<
∴
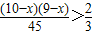 …(10分)
…(10分)解得:x<4或x>15(舍),故该考生最多会3道题…(13分)
点评:本题主要考查了等可能事件的概率,以及离散型随机变量及其分布列和数学期望,同时考查了计算能力,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
 ,那么他最多会几道题?
,那么他最多会几道题?