题目内容
某大学2009届入学测试中,要求每位考生在10道题中随机抽出2道题回答.
(I)现在某位考生会答10道题中的6道,求这个考生答错题目个数的分布列和数学期望;
(II)若答对其中一题即为及格,如果某位考生及格的概率小于 ,那么他最多会几道题?
,那么他最多会几道题?
(II)若答对其中一题即为及格,如果某位考生及格的概率小于
 ,那么他最多会几道题?
,那么他最多会几道题?解:(1)答错题目的个数 =0,1,2
=0,1,2
P( =0)=
=0)= =
= ,P(
,P( =1)=
=1)= =
= ,P(
,P( =2)=
=2)= =
=
分布列为:

期望E =0
=0
 +1
+1
 +2
+2
 =
= (道题)
(道题)
(2)设该考生会x道题,不会10﹣x道题,
则1﹣ <
<

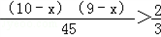
解得:x<4或x>15(舍),故该考生最多会3道题
 =0,1,2
=0,1,2P(
 =0)=
=0)= =
= ,P(
,P( =1)=
=1)= =
= ,P(
,P( =2)=
=2)= =
=
分布列为:

期望E
 =0
=0
 +1
+1
 +2
+2
 =
= (道题)
(道题)(2)设该考生会x道题,不会10﹣x道题,
则1﹣
 <
<

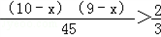
解得:x<4或x>15(舍),故该考生最多会3道题

练习册系列答案
相关题目
 ,那么他最多会几道题?
,那么他最多会几道题?