题目内容
已知集合P={x|x2-4x+3=0}，S={x|ax+3=0}且S∩P=S，则a=________．
-1，-3或0
分析：首先对集合P进行化简求解，然后对SA分情况分析，然后根据S∩P=S求出满足题意的a的值即可．
解答：∵P={x|x2-4x+3=0}，
解得：P={1，3}
∵S={x|ax+3=0}
①当a=0时，S=∅
②当a≠0时，S={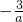
}
∵S∩P=S
∴S⊆P
∴当a=0时，S=∅满足题意
当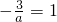
时，a=-3，满足题意
当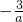=3时，a=-1，满足题意
故答案为：-1，-3或0．
点评：本题考查交集及其运算，通过对集合元素的知识的熟练掌握与应用，灵活解决问题，属于基础题．
分析：首先对集合P进行化简求解，然后对SA分情况分析，然后根据S∩P=S求出满足题意的a的值即可．
解答：∵P={x|x2-4x+3=0}，
解得：P={1，3}
∵S={x|ax+3=0}
①当a=0时，S=∅
②当a≠0时，S={
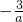}∵S∩P=S
∴S⊆P
∴当a=0时，S=∅满足题意
当
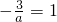时，a=-3，满足题意当
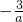=3时，a=-1，满足题意故答案为：-1，-3或0．
点评：本题考查交集及其运算，通过对集合元素的知识的熟练掌握与应用，灵活解决问题，属于基础题．
练习册系列答案
相关题目
已知集合P={x|x（x-1）≥0}，Q={x|
＞0}，则P∩Q等于（ ）
| 1 |
| x-1 |
| A、∅ |
| B、{x|x≥1} |
| C、{x|x＞1} |
| D、{x|x≥1或x＜0} |