题目内容
已知函数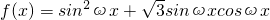 (ω>0)图象的两相邻对称轴间的距离为
(ω>0)图象的两相邻对称轴间的距离为 .
.
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)的单调减区间;
(Ⅲ)若对任意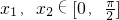 都有|f(x1)-f(x2)|<m,求实数m的取值范围.
都有|f(x1)-f(x2)|<m,求实数m的取值范围.
解:(Ⅰ)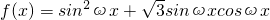 =
=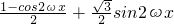 =sin(2ωx-
=sin(2ωx- )+
)+ ,
,
∵函数图象的两相邻对称轴间的距离为 ,故
,故  =
= ,∴ω=2.
,∴ω=2.
(Ⅱ)由(Ⅰ)知f(x)=sin(4x- )+
)+ ,∵
,∵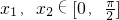 ,-
,- ≤4x1-
≤4x1- ≤
≤ ,
,
- ≤4x2-
≤4x2- ≤
≤ ,∴当4x-
,∴当4x- =
= 时,f(x)最大为 1+
时,f(x)最大为 1+ =
= ,
,
当4x- =
= 时,f(x)最小为-1+
时,f(x)最小为-1+ =-
=- ,故|f(x1)-f(x2)|的最大值等于
,故|f(x1)-f(x2)|的最大值等于 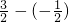 =2,
=2,
故m>2,实数m的取值范围为(2,+∞).
分析:(Ⅰ)化简f(x)的解析式为sin(2ωx- )+
)+ ,根据函数图象的两相邻对称轴间的距离为
,根据函数图象的两相邻对称轴间的距离为 ,故
,故  =
= ,解得ω的值
,解得ω的值
(Ⅱ)根据角的范围求得f(x)最大值和最小值,得到|f(x1)-f(x2)|的最大值等于 2,故m>2.
点评:本题考查两角差的正弦公式,正弦函数的单调性,周期性,三角函数的最值,求出|f(x1)-f(x2)|的最大值,是
解题的难点.
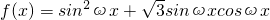 =
=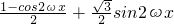 =sin(2ωx-
=sin(2ωx- )+
)+ ,
,∵函数图象的两相邻对称轴间的距离为
 ,故
,故  =
= ,∴ω=2.
,∴ω=2.(Ⅱ)由(Ⅰ)知f(x)=sin(4x-
 )+
)+ ,∵
,∵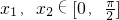 ,-
,- ≤4x1-
≤4x1- ≤
≤ ,
,-
 ≤4x2-
≤4x2- ≤
≤ ,∴当4x-
,∴当4x- =
= 时,f(x)最大为 1+
时,f(x)最大为 1+ =
= ,
,当4x-
 =
= 时,f(x)最小为-1+
时,f(x)最小为-1+ =-
=- ,故|f(x1)-f(x2)|的最大值等于
,故|f(x1)-f(x2)|的最大值等于 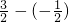 =2,
=2,故m>2,实数m的取值范围为(2,+∞).
分析:(Ⅰ)化简f(x)的解析式为sin(2ωx-
 )+
)+ ,根据函数图象的两相邻对称轴间的距离为
,根据函数图象的两相邻对称轴间的距离为 ,故
,故  =
= ,解得ω的值
,解得ω的值(Ⅱ)根据角的范围求得f(x)最大值和最小值,得到|f(x1)-f(x2)|的最大值等于 2,故m>2.
点评:本题考查两角差的正弦公式,正弦函数的单调性,周期性,三角函数的最值,求出|f(x1)-f(x2)|的最大值,是
解题的难点.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 已知函数f(x)的图象如图所示,f′(x)是函数f(x)的导函数,且y=f(x+1)是奇函数,那么下列结论中错误的是( )
已知函数f(x)的图象如图所示,f′(x)是函数f(x)的导函数,且y=f(x+1)是奇函数,那么下列结论中错误的是( )
 (其中A>0,
(其中A>0, )的图象如图所示.
)的图象如图所示. ,求
,求 的值.
的值.
 (x〉0)的图象与x轴的交点从左到右依次为
(x〉0)的图象与x轴的交点从左到右依次为 则数列
则数列 的前4项和为_______.
的前4项和为_______.