题目内容
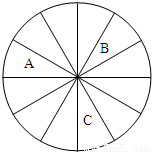
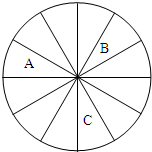 某商场进行促销活动,到商场购物消费满100元就可转动转盘(转盘为十二等分的圆盘)一次进行抽奖,满200元转两次,以此类推(奖金累加);转盘的指针落在A区域中一等奖,奖10元,落在B、C区域中二等奖,奖5元,落在其它区域则不中奖.一位顾客一次购物消费268元,
某商场进行促销活动,到商场购物消费满100元就可转动转盘(转盘为十二等分的圆盘)一次进行抽奖,满200元转两次,以此类推(奖金累加);转盘的指针落在A区域中一等奖,奖10元,落在B、C区域中二等奖,奖5元,落在其它区域则不中奖.一位顾客一次购物消费268元,(Ⅰ)求该顾客中一等奖的概率;
(Ⅱ)记ξ为该顾客所得的奖金数,求其分布列;
(Ⅲ)求数学期望Eξ(精确到0.01).
分析:(I)该顾客中一等奖分为以下两种情况,一是两次均中一等奖,二是两次有且只有一次中一等奖,由于每次中一等奖概率为
,代入相互独立事件概率乘法公式,结合互斥事件概率加法公式,即可得到答案.
(II)由于该顾客可以转两次,故ξ的可能取值为20,15,10,5,0,分别计算出对应的概率,即可得到随机变量ξ的分布列;
(III)根据(II)的结论中随机变量ξ的分布列,代入数学期望公式,即可求出数学期望Eξ.
| 1 |
| 12 |
(II)由于该顾客可以转两次,故ξ的可能取值为20,15,10,5,0,分别计算出对应的概率,即可得到随机变量ξ的分布列;
(III)根据(II)的结论中随机变量ξ的分布列,代入数学期望公式,即可求出数学期望Eξ.
解答:解:(Ⅰ)设事件A表示该顾客中一等奖
P(A)=
×
+2×
×
=
所以该顾客中一等奖的概率是
(4分)
(Ⅱ)ξ的可能取值为20,15,10,5,0(5分)
P(ξ=20)=
×
=
,P(ξ=15)=2×
×
=
,
P(ξ=10)=
×
+2×
×
=
P(ξ=5)=2×
×
=
,
P(ξ=0)=
×
=
(每个1分)(10分)
所以ξ的分布列为
(10分)
(Ⅲ)数学期望Eξ=20×
+15×
+10×
+5×
≈3.33(14分)
P(A)=
| 1 |
| 12 |
| 1 |
| 12 |
| 1 |
| 12 |
| 11 |
| 12 |
| 23 |
| 144 |
所以该顾客中一等奖的概率是
| 23 |
| 144 |
(Ⅱ)ξ的可能取值为20,15,10,5,0(5分)
P(ξ=20)=
| 1 |
| 12 |
| 1 |
| 12 |
| 1 |
| 144 |
| 1 |
| 12 |
| 2 |
| 12 |
| 1 |
| 36 |
P(ξ=10)=
| 2 |
| 12 |
| 2 |
| 12 |
| 1 |
| 12 |
| 9 |
| 12 |
| 11 |
| 72 |
| 2 |
| 12 |
| 9 |
| 12 |
| 1 |
| 4 |
P(ξ=0)=
| 9 |
| 12 |
| 9 |
| 12 |
| 9 |
| 16 |
所以ξ的分布列为
| ξ | 20 | 15 | 10 | 5 | 0 | ||||||||||
| P |
|
|
|
|
|
(Ⅲ)数学期望Eξ=20×
| 1 |
| 144 |
| 1 |
| 36 |
| 11 |
| 72 |
| 1 |
| 4 |
点评:本题考查的知识点是相互独立事件概率乘法公式、互斥事件的概率加法公式、离散型随机变量及其分布列、离散型随机变量的期望,其中根据顾客一次购物消费268元,计算出转盘次数,并给出ξ的可能取值,是解答本题的关键.

练习册系列答案
相关题目
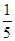 ,若中奖,则商场返还顾客现金100元某顾客购买价格为340元的商品,得到3张奖券(I)求商场恰好返还该顾客现金100元的概率;
,若中奖,则商场返还顾客现金100元某顾客购买价格为340元的商品,得到3张奖券(I)求商场恰好返还该顾客现金100元的概率;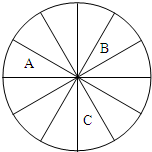 某商场进行促销活动,到商场购物消费满100元就可转动转盘(转盘为十二等分的圆盘)一次进行抽奖,满200元转两次,以此类推(奖金累加);转盘的指针落在A区域中一等奖,奖10元,落在B、C区域中二等奖,奖5元,落在其它区域则不中奖.一位顾客一次购物消费268元,
某商场进行促销活动,到商场购物消费满100元就可转动转盘(转盘为十二等分的圆盘)一次进行抽奖,满200元转两次,以此类推(奖金累加);转盘的指针落在A区域中一等奖,奖10元,落在B、C区域中二等奖,奖5元,落在其它区域则不中奖.一位顾客一次购物消费268元,