题目内容
已知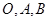 是平面上的三个点,直线
是平面上的三个点,直线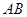 上有一点
上有一点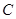 满足
满足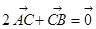 ,则
,则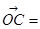 ( )
( )
A. | B. | C.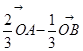 | D.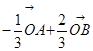 |
A
解析试题分析:本小题主要考查平面向量的基本定理,把一个向量用平面上的两个不共线的向量来表示,这两个不共线的向量作为一组基底参与向量的运算,注意题目给的等式的应用.根据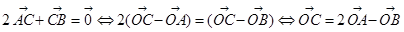 ,那吗可知三点共线,故选A.
,那吗可知三点共线,故选A.
考点:向量之间的运算
点评:本题是向量之间的运算,运算过程简单,但应用广泛,向量具有代数特征和几何特征,借助于向量可以实现某些代数问题与几何问题的相互转化.

练习册系列答案
相关题目
已知平面向量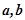 的夹角为
的夹角为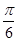 ,且
,且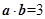 ,
,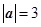 ,则
,则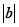 等于( )
等于( )
A. | B.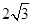 | C.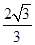 | D. |
已知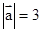 ,
,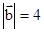 ,且(
,且(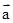 +k
+k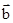 )⊥(
)⊥(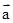
 k
k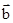 ),则k等于 ( )
),则k等于 ( )
A.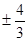 | B.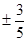 | C.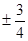 | D.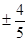 |
已知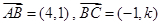 ,若A,B,C三点共线,则实数k的值为 ( )
,若A,B,C三点共线,则实数k的值为 ( )
A.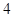 | B.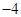 | C.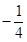 | D.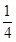 |
平面向量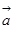 与
与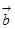 的夹角为
的夹角为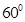 ,
,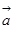 =(2,0),
=(2,0),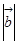 ="1" 则
="1" 则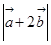 =( )
=( )
A. | B.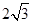 | C.4 | D.12 |
已知a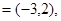 b=
b=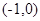 ,向量
,向量 垂直,则实数
垂直,则实数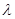 的值为( )
的值为( )
A.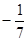 | B.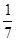 | C.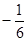 | D.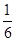 |
如图,D为等腰三角形ABC底边AB的中点,则下列等式恒成立的是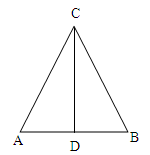
A. | B.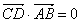 |
C.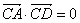 | D.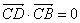 |
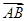 ·
·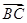 =3,△ABC的面积S∈[
=3,△ABC的面积S∈[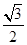 ,
, ],则
],则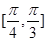
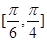
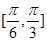
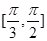
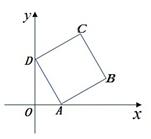
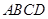 的顶点
的顶点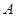 ,
,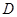 分别在
分别在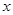 轴、
轴、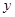 轴正半轴上移动,则
轴正半轴上移动,则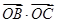 的最大值是( )
的最大值是( )