题目内容
已知函数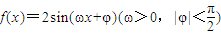 的最小正周期为π,且在
的最小正周期为π,且在 处取得最大值.
处取得最大值.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,若
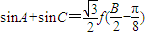 ,且
,且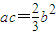 ,求角B.
,求角B.
【答案】分析:(Ⅰ)由已知函数的周期,利用三角函数的周期公式求出ω的值,再由函数在 处取得最大值,得到点(
处取得最大值,得到点(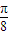 ,2)在函数图象上,将此点代入函数解析式中确定出φ的值,即可确定出函数f(x)的解析式;
,2)在函数图象上,将此点代入函数解析式中确定出φ的值,即可确定出函数f(x)的解析式;
(Ⅱ)利用第一问确定出的函数解析式化简已知的等式sinA+sinC= f(
f(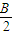 -
- ),再利用正弦定理变形,表示出a+c,利用余弦定理表示出cosB,将表示出的a+c及ac代入,化简后得出cosB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数.
),再利用正弦定理变形,表示出a+c,利用余弦定理表示出cosB,将表示出的a+c及ac代入,化简后得出cosB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数.
解答:解:(Ⅰ)∵f(x)的最小正周期为π,
∴ =π,即ω=2,
=π,即ω=2,
∴f(x)=2sin(2x+φ),
又点( ,2)在函数图象上,得sin(
,2)在函数图象上,得sin( +φ)=1,
+φ)=1,
∵|φ|<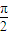 ,∴φ=
,∴φ= ,
,
则f(x)的解析式为f(x)=2sin(2x+ );
);
(Ⅱ)由sinA+sinC= f(
f(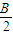 -
- ),得sinA+sinC=
),得sinA+sinC=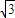 sinB,
sinB,
由正弦定理得:a+c= b,又ac=
b,又ac= b2,
b2,
由余弦定理得:cosB= =
=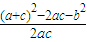 =
=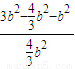 =
= ,
,
∵0<B<π,∴B= .
.
点评:此题考查了正弦、余弦定理,三角函数y=Asin(ωx+φ)解析式的确定,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.
 处取得最大值,得到点(
处取得最大值,得到点(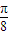 ,2)在函数图象上,将此点代入函数解析式中确定出φ的值,即可确定出函数f(x)的解析式;
,2)在函数图象上,将此点代入函数解析式中确定出φ的值,即可确定出函数f(x)的解析式;(Ⅱ)利用第一问确定出的函数解析式化简已知的等式sinA+sinC=
 f(
f(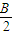 -
- ),再利用正弦定理变形,表示出a+c,利用余弦定理表示出cosB,将表示出的a+c及ac代入,化简后得出cosB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数.
),再利用正弦定理变形,表示出a+c,利用余弦定理表示出cosB,将表示出的a+c及ac代入,化简后得出cosB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数.解答:解:(Ⅰ)∵f(x)的最小正周期为π,
∴
 =π,即ω=2,
=π,即ω=2,∴f(x)=2sin(2x+φ),
又点(
 ,2)在函数图象上,得sin(
,2)在函数图象上,得sin( +φ)=1,
+φ)=1,∵|φ|<
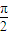 ,∴φ=
,∴φ= ,
,则f(x)的解析式为f(x)=2sin(2x+
 );
);(Ⅱ)由sinA+sinC=
 f(
f(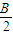 -
- ),得sinA+sinC=
),得sinA+sinC=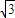 sinB,
sinB,由正弦定理得:a+c=
 b,又ac=
b,又ac= b2,
b2,由余弦定理得:cosB=
 =
=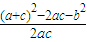 =
=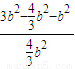 =
= ,
,∵0<B<π,∴B=
 .
.点评:此题考查了正弦、余弦定理,三角函数y=Asin(ωx+φ)解析式的确定,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 的最小正周期为
的最小正周期为 ,将其图象向左平移
,将其图象向左平移 个单位长度,所得图象关于
个单位长度,所得图象关于 轴对称,则
轴对称,则 的一个可能值是
( )
的一个可能值是
( ) B.
B. C.
C. D.
D.
 的最小正周期为2π.
的最小正周期为2π. ,求
,求 的值.
的值. 的最小正周期为π,其图象关于直线
的最小正周期为π,其图象关于直线 对称.
对称. 上的单调递增区间;
上的单调递增区间; 上只有一个实数解,求实数m的取值范围.
上只有一个实数解,求实数m的取值范围. 的最小正周期为
的最小正周期为 .
. 的值;
的值; 的最小正周期为
的最小正周期为
 的值;
的值;
 在
在
 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.