题目内容
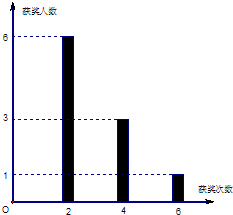 某校高二(1)班的数学兴趣小组共有10人,他们参加数学竞赛获奖次数统计如图所示.
某校高二(1)班的数学兴趣小组共有10人,他们参加数学竞赛获奖次数统计如图所示.(I)求数学兴趣小组学生获奖的人均次数;
(II)从数学兴趣小组中任意选两名学生,求他们获奖次数恰好相等的概率.
(III)从数学兴趣小组中任意选两名学生,求他们获奖次数都超过三次的概率.
分析:(I)数学兴趣小组学生获奖的人均次数为
,运算求得结果.
(II)所有的情况有
个,“获奖次数恰好相等”这一基本事件共有
+
个,由此求得他们获奖次数恰好相等的概率.
(III他们获奖次数都超过三次的选法有
=6个,而所有的情况有
=45 个,由此求得他们获奖次数都超过三次的概率.
| 2×6+4×3+6×1 |
| 10 |
(II)所有的情况有
| C | 2 10 |
| C | 2 6 |
| C | 2 3 |
(III他们获奖次数都超过三次的选法有
| C | 2 4 |
| C | 2 10 |
解答:解:(I)数学兴趣小组学生获奖的人均次数为
=3.
(II)所有的情况有
=45 个,“获奖次数恰好相等”这一基本事件共有
+
=18个,
因而,他们获奖次数恰好相等的概率为
=
.
(III)“获奖次数都超过三次”的学生共计有4个人,从数学兴趣小组中任意选两名学生,
他们获奖次数都超过三次的选法有
=6个,
所有的情况有
=45 个,故他们获奖次数都超过三次的概率为
=
.
| 2×6+4×3+6×1 |
| 10 |
(II)所有的情况有
| C | 2 10 |
| C | 2 6 |
| C | 2 3 |
因而,他们获奖次数恰好相等的概率为
| 18 |
| 45 |
| 2 |
| 5 |
(III)“获奖次数都超过三次”的学生共计有4个人,从数学兴趣小组中任意选两名学生,
他们获奖次数都超过三次的选法有
| C | 2 4 |
所有的情况有
| C | 2 10 |
| 6 |
| 45 |
| 2 |
| 15 |
点评:本题考查古典概型及其概率计算公式的应用,属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目



 之间的频数;
之间的频数;
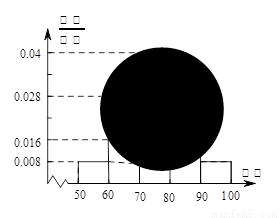
 之间的频数;
之间的频数;

 之间的频数;
之间的频数; 间的矩形的高.
间的矩形的高.