题目内容
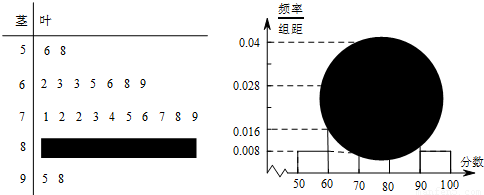
某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题.

(1)求全班人数,并求出分数在[80,90)之间的频数;
(2)估计该班的平均分数,并计算频率分布直方图中[80,90)间的矩形的高.

(1)求全班人数,并求出分数在[80,90)之间的频数;
(2)估计该班的平均分数,并计算频率分布直方图中[80,90)间的矩形的高.
分析:(1)根据茎叶图的数据,计算出分数在[80,90)之间的频数.
(2)根据数据计算出平均数,然后计算出频率分布直方图中[80,90)间的矩形的高.
(2)根据数据计算出平均数,然后计算出频率分布直方图中[80,90)间的矩形的高.
解答:解:(1)由茎叶图知,分数在[50,60)之间的频数为2,频率为0.008×10=0.08,
全班人数为
=25. …(3分)
所以分数在[80,90)之间的频数为25-2-7-10-2=4…(6分)
(2)分数在[50,60)之间的总分为56+58=114;
分数在[60,70)之间的总分为60×7+2+3+3+5+6+8+9=456;
分数在[70,80)之间的总分数为70×10+1+2+3+3+4+5+6+7+8+9=747;
分数在[80,90)之间的总分约为85×4=340;
分数在[90,100]之间的总分数为95+98=193;
所以,该班的平均分数为
=74. …(9分)
注:估计平均分时,以下解法也给分:
分数在[50,60)之间的频率为
=0.08; 分数在[60,70)之间的频率为
=0.28;
分数在[70,80)之间的频率为
=0.40;分数在[80,90)之间的频率为
=0.16;
分数在[90,100]之间的频率为
=0.08;
所以,该班的平均分约为55×0.08+65×0.28+75×0.40+85×0.16+95×0.08=73.8
频率分布直方图中[80,90)间的矩形的高为
÷10=0.016. …(12分)
全班人数为
| 2 |
| 0.08 |
所以分数在[80,90)之间的频数为25-2-7-10-2=4…(6分)
(2)分数在[50,60)之间的总分为56+58=114;
分数在[60,70)之间的总分为60×7+2+3+3+5+6+8+9=456;
分数在[70,80)之间的总分数为70×10+1+2+3+3+4+5+6+7+8+9=747;
分数在[80,90)之间的总分约为85×4=340;
分数在[90,100]之间的总分数为95+98=193;
所以,该班的平均分数为
| 114+456+747+340+193 |
| 25 |
注:估计平均分时,以下解法也给分:
分数在[50,60)之间的频率为
| 2 |
| 25 |
| 7 |
| 25 |
分数在[70,80)之间的频率为
| 10 |
| 25 |
| 4 |
| 25 |
分数在[90,100]之间的频率为
| 2 |
| 25 |
所以,该班的平均分约为55×0.08+65×0.28+75×0.40+85×0.16+95×0.08=73.8
频率分布直方图中[80,90)间的矩形的高为
| 4 |
| 25 |
点评:本题主要考查茎叶图的应用,以及频率分别直方图的应用,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


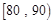 之间的频数;
之间的频数;
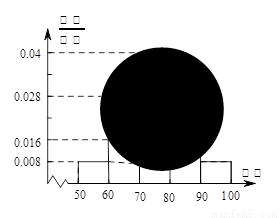
 之间的频数;
之间的频数;

 之间的频数;
之间的频数; 间的矩形的高.
间的矩形的高.