题目内容
已知P点坐标为(2,3),在y轴及直线y=
x上各取一点R、Q,为使△PQR的周长最小,则Q点的坐标为
| 1 |
| 2 |
(
,
)
| 13 |
| 30 |
| 13 |
| 15 |
(
,
)
,R点的坐标为| 13 |
| 30 |
| 13 |
| 15 |
(0,
)
| 13 |
| 7 |
(0,
)
.| 13 |
| 7 |
分析:设点P(2,3)关于直线y=
x的对称点为P′(m,n),则
,解得即可得P′.易求P(2,3)关于y轴的对称点P′′(-2,3),可得kP′P″.直线P′P″的方程为y-3=-
(x+2),令x=0,解得y,得R.联立直线y=
x与直线P′P″的方程得Q.
| 1 |
| 2 |
|
| 4 |
| 7 |
| 1 |
| 2 |
解答:解:如图所示.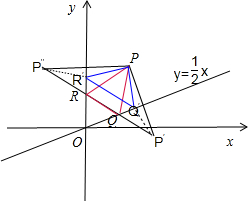
设点P(2,3)关于直线y=
x的对称点为P′(m,n),则
,解得
.
∴P′(
,-
).
求P(2,3)关于y轴的对称点P″(a,b),则
,解得a=-2,b=3,∴P′′(-2,3),
∴kP′P″=
=-
.
∴直线P′P″的方程为y-3=-
(x+2),化为4x+7y-13=0.
令x=0,解得y=
,得R(0,
).
联立
,解得
.∴Q(
,
).
下面证明所求的R(0,
),Q(
,
)满足题意.
如图所示,△PQR的周长=|P′P″|.
当R点是y轴上的另一点R′或点Q是另一点Q′时,则△PQ′R′的周长=|P″R′|+|R′Q′|+|P′Q′|>|P′P″|,
因此△PQR的周长=|P′P″|是最小值.
故答案为Q(
,
),R(0,
).

设点P(2,3)关于直线y=
| 1 |
| 2 |
|
|
∴P′(
| 18 |
| 5 |
| 1 |
| 5 |
求P(2,3)关于y轴的对称点P″(a,b),则
|
∴kP′P″=
-
| ||
|
| 4 |
| 7 |
∴直线P′P″的方程为y-3=-
| 4 |
| 7 |
令x=0,解得y=
| 13 |
| 7 |
| 13 |
| 7 |
联立
|
|
| 13 |
| 30 |
| 13 |
| 15 |
下面证明所求的R(0,
| 13 |
| 7 |
| 13 |
| 30 |
| 13 |
| 15 |
如图所示,△PQR的周长=|P′P″|.
当R点是y轴上的另一点R′或点Q是另一点Q′时,则△PQ′R′的周长=|P″R′|+|R′Q′|+|P′Q′|>|P′P″|,
因此△PQR的周长=|P′P″|是最小值.
故答案为Q(
| 13 |
| 30 |
| 13 |
| 15 |
| 13 |
| 7 |
点评:本题考查了点关于直线的对称点的求法、三角形周长最小值问题等基础知识与基本技能方法,属于难题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 椭圆C1,抛物线C2的焦点均在x轴上,从两条曲线上各取两个点,将其坐标混合记录于下表中:
椭圆C1,抛物线C2的焦点均在x轴上,从两条曲线上各取两个点,将其坐标混合记录于下表中: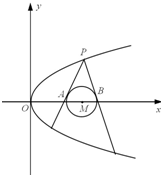 (2013•杭州一模)已知抛物线C:y2=2px(p>0)和⊙M:x2+y2+8x-12=0,过抛物线C上一点P(x0,y0)(y0≥0)作两条直线与⊙M相切与A、B两点,圆心M到抛物线准线的距离为
(2013•杭州一模)已知抛物线C:y2=2px(p>0)和⊙M:x2+y2+8x-12=0,过抛物线C上一点P(x0,y0)(y0≥0)作两条直线与⊙M相切与A、B两点,圆心M到抛物线准线的距离为