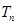题目内容
20、 (本小题14分)
已知函数y=x2-2ax+1(a为常数)在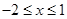 上的最小值为
上的最小值为 ,
,
试将 用a表示出来,并求出
用a表示出来,并求出 的最大值.
的最大值.
【答案】
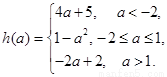
 .
.
【解析】解决二次函数的最值问题,应该先求出二次函数的对称轴,判断出对称轴与区间的关系,进一步判断出二次函数的单调性,进一步求出函数的最值.由该函数的性质可知,该函数的最小值与抛物线的对称轴的位置有关,于是需要对对称轴的位置进行分类讨论.
解:∵y=(x-a)2+1-a2,
∴抛物线y=x2-2ax+1的对称轴方程是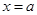 .
.
(1)当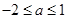 时,由图①可知,当
时,由图①可知,当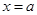 时,该函数取最小值
时,该函数取最小值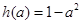 ;
;
(2) 当 时, 由图②可知, 当
时, 由图②可知, 当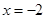 时,该函数取最小值
时,该函数取最小值 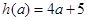 ;
;
(3) 当a>1时, 由图③可知, 当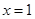 时,该函数取最小值
时,该函数取最小值
综上,函数的最小值为
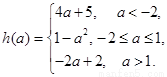 ………………8分
………………8分
 (1)当
(1)当 时,
时,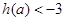
⑵当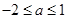 时,
时,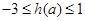
⑶当a>1时,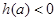 ,
,
综上所述, .
………………14分
.
………………14分

练习册系列答案
相关题目
 (本小题14分)右图是一个直三棱柱(以
(本小题14分)右图是一个直三棱柱(以
 km,用
km,用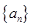 中,
中,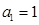 ,前
,前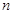 项和
项和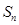 满足条件
满足条件 ,
,
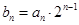 ,求数列
,求数列 的前
的前