题目内容
观察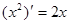 ,
,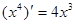 ,
,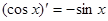 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在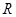 上的函数
上的函数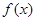 满足
满足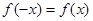 ,记
,记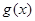 为
为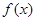 的导函数,则
的导函数,则 ( )
( )
A.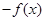 | B.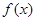 | C.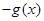 | D.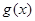 |
C
解析试题分析:因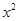 ,
,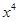 ,
,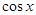 都是偶函数,其导数
都是偶函数,其导数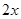 ,
,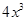 ,
,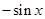 都是奇函数,故可归纳得偶函数的导数为奇函数,由
都是奇函数,故可归纳得偶函数的导数为奇函数,由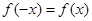 知
知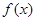 是偶函数,故其导数
是偶函数,故其导数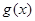 为奇函数,所以
为奇函数,所以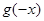 =
=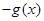 ,故选C.
,故选C.
考点:函数奇偶性;推理证明

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知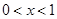 ,则
,则 取得最大值时
取得最大值时 的值为( )
的值为( )
A. | B. | C. | D.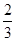 |
函数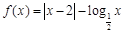 的零点个数为 ( )
的零点个数为 ( )
| A.0 | B.1 | C.2 | D.3 |
已知定义在R上的函数f(x)的周期为4,且当x∈(-1,3]时,f(x)=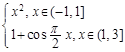 ,则函数
,则函数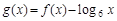 的零点个数是( )
的零点个数是( )
| A.4 | B.5 | C.6 | D.7 |
已知 在区间(0,+∞)上是减函数,那么
在区间(0,+∞)上是减函数,那么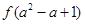 与
与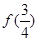 的大小关系是( ).
的大小关系是( ).
A.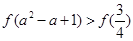 | B. |
C.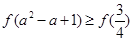 | D.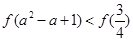 |
若函数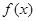 的零点与
的零点与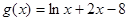 的零点之差的绝对值不超过
的零点之差的绝对值不超过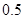 , 则
, 则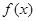 可以是( )
可以是( )
A.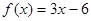 | B.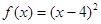 |
C.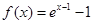 | D.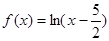 |
下列函数中,既是偶函数,又是在区间(0,+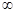 )上单调递减的函数是( )
)上单调递减的函数是( )
A. | B.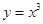 | C.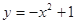 | D.y=cosx |
 的图象大致是( ).
的图象大致是( ).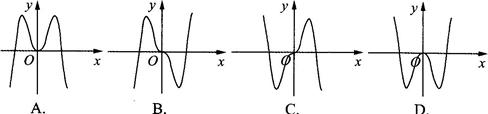
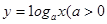 ,且
,且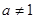 )的图像如右图所示,则下列函数图像正确的是
)的图像如右图所示,则下列函数图像正确的是