题目内容
如图所示的一组图形为某一四棱锥S―ABCD的侧面与底面；
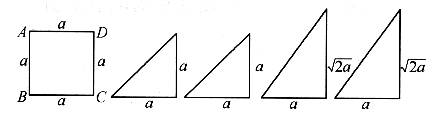
(1)请画出四棱锥S―ABCD的示意图，并判断是否存在一条侧棱垂直于底面?如果存在，请给出证明；
(2)若SA⊥平面ABCD，E为AB中点，求二面角E―SC―D的大小；
(3)在(2)的条件下，求点D到平面SEC的距离．
解：(1)如图a所示，存在一条侧棱SA⊥平面ABCD．
∴在△SAB中，SA⊥AB，在△SAD中，SA⊥AD，
∴SA⊥平面ABCD
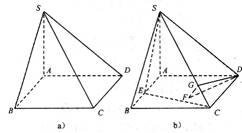
(2)设点D在平面SEC上的射影为F，
过F作FG⊥SC于点G，连接DG，如图b所示，则有DG⊥SC．
因为SA?S△DEC=DF?S△SEC，所以DF=
，
又DG=
=
==DF
(F、G同在平面SEC内，且DF⊥平面SEC)，
所以二面角E―SC―D=90?．
(3)由(2)得DF=．
练习册系列答案
相关题目
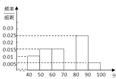，50），[50，60），…[90，100]后画出如图所示的部分频率分布直方图．观察图形的信息，回答下列问题：
，50），[50，60），…[90，100]后画出如图所示的部分频率分布直方图．观察图形的信息，回答下列问题：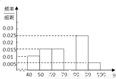
，50），[50，60），…[90，100]后画出如图所示的部分频率分布直方图．观察图形的信息，回答下列问题：