题目内容
已知数列1,11,111,1111, ,
, ,
, ,写出该数列的一个通项公式,并用反证法证明该数列中每一项都不是完全平方数.
,写出该数列的一个通项公式,并用反证法证明该数列中每一项都不是完全平方数.
 ,
, ,
, ,写出该数列的一个通项公式,并用反证法证明该数列中每一项都不是完全平方数.
,写出该数列的一个通项公式,并用反证法证明该数列中每一项都不是完全平方数.数列的一个通项公式是

由于 ,所以该数列的一个通项公式是
,所以该数列的一个通项公式是 ;
;
证明:假设 是一个完全平方数,由于
是一个完全平方数,由于 是一个奇数,所以它必须是一个奇数的平方,不妨设
是一个奇数,所以它必须是一个奇数的平方,不妨设 (
( 为整数),于是
为整数),于是 .故
.故 此式中左边是奇数,右边是偶数,自相矛盾,所以
此式中左边是奇数,右边是偶数,自相矛盾,所以 不是一个完全平方数.
不是一个完全平方数.
 ,所以该数列的一个通项公式是
,所以该数列的一个通项公式是 ;
;证明:假设
 是一个完全平方数,由于
是一个完全平方数,由于 是一个奇数,所以它必须是一个奇数的平方,不妨设
是一个奇数,所以它必须是一个奇数的平方,不妨设 (
( 为整数),于是
为整数),于是 .故
.故 此式中左边是奇数,右边是偶数,自相矛盾,所以
此式中左边是奇数,右边是偶数,自相矛盾,所以 不是一个完全平方数.
不是一个完全平方数.
练习册系列答案
相关题目
 .
. ;
; .
. ,(
,( ,
, 为虚单位)。
为虚单位)。 为实数,求
为实数,求 的值;
的值;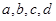 满足
满足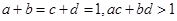 ,求证
,求证 (本小题12分)
(本小题12分) 且
且 ,求证
,求证 和
和 中至少有一个成立。
中至少有一个成立。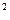 -y
-y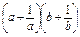 ≥
≥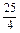 .
. 证明:
证明: 
 ……是无限的
……是无限的