题目内容
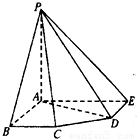
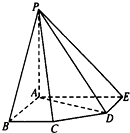
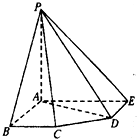 如图,在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=
如图,在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=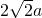 ,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
(1)求证:PA⊥平面ABCDE;
(2)求异面直线CD与PB所成角的大小;
(3)求二面角A-PD-E的大小.
 解:(1)∵PA=AE=2a,PB=PE=
解:(1)∵PA=AE=2a,PB=PE=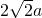
∴PA2+AB2=PB2,
∴∠PAB=90°,
即PA⊥AB
同理PA⊥AE
∵AB∩AE=A,
∴PA⊥平面ABCDE
(2)由CD∥BE,
则∠PBE即为所求角
又PB=PE=BE=
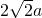
∴∠PBE=60°
(3)∵∠AED=90°,
∴AE⊥ED
∵PA⊥平面ABCDE,
∴PA⊥ED
∴ED⊥平面PAE
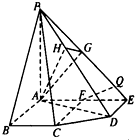
如图,过A作AG⊥PE于G,
∴DE⊥AG,
∴AG⊥平面PDE
过G作GH⊥PD于H,连接AH,
由三垂线定理得AH⊥PD
∴∠AHG为二面角A-PD-E的平面角
在Rt△PAE中,
 ,
,在Rt△PAD中,
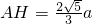
∴在Rt△AHG中,
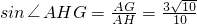
∴
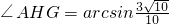
∴二面角A-PD-E的大小为
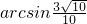
分析:(1)要证明PA⊥平面ABCDE,只需证明PA⊥AB,PA⊥AE,AB∩AE=A,通过定理即可得到结论;
(2)说明∠PBE即为异面直线CD与PB所成角的大小,通过三角形即可得到结果;
(3)如图,过A作AG⊥PE于G,过G作GH⊥PD于H,连接AH,说明∠AHG为二面角A-PD-E的平面角,在Rt△AHG中,求出二面角A-PD-E的大小.
点评:本题是中档题,考查直线与平面的垂直,直线与平面所成的角,平面与平面所成的角的求法,考查空间想象能力,计算能力,转化思想.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
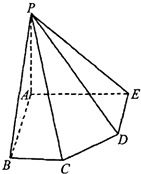
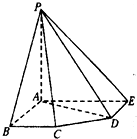 如图,在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=
如图,在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=
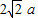 ,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.