题目内容
坐标平面上满足方程式(| x2 |
| 52 |
| y2 |
| 42 |
| x2 |
| 32 |
| y2 |
| 42 |
（1）只有原点
（2）椭圆及原点
（3）两条相异直线
（4）椭圆及双曲线
（5）双曲线及原点．
分析：把方程变形为 (
+
)(
-
)(
+
)=0，
+
=0 表示点（0，0），而
-
=0 和
+
=0
代表相交于（0，0）的两相异直线，由此得出结论．
| x2 |
| 52 |
| y2 |
| 42 |
| x |
| 3 |
| y |
| 4 |
| x |
| 3 |
| y |
| 4 |
| x2 |
| 52 |
| y2 |
| 42 |
| x |
| 3 |
| y |
| 4 |
| x |
| 3 |
| y |
| 4 |
代表相交于（0，0）的两相异直线，由此得出结论．
解答：解：由(
+
)(
-
)=0得 (
+
)(
-
)(
+
)=0，
即
+
=0或
-
=0或
+
=0，
由
+
=0得x=y=0，表示点（0，0 ）．
而
-
=0，
+
=0代表相交于（0，0）的两相异直线，
故答案为（3）．
| x2 |
| 52 |
| y2 |
| 42 |
| x2 |
| 32 |
| y2 |
| 42 |
| x2 |
| 52 |
| y2 |
| 42 |
| x |
| 3 |
| y |
| 4 |
| x |
| 3 |
| y |
| 4 |
即
| x2 |
| 52 |
| y2 |
| 42 |
| x |
| 3 |
| y |
| 4 |
| x |
| 3 |
| y |
| 4 |
由
| x2 |
| 52 |
| y2 |
| 42 |
而
| x |
| 3 |
| y |
| 4 |
| x |
| 3 |
| y |
| 4 |
故答案为（3）．
点评：本题考查方程表示的曲线，把方程变形，是解题的关键．
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
相关题目
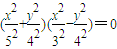的点（x，y）所构成的图形为