题目内容
若x2+xy+y2=1且x、y∈R,则n=x2+y2的取值范围是( )
| A.0<n≤1 | B.2≤n≤3 |
| C.n≥2 | D.≤n≤2 |
D
分析:先根据x2+xy+y2=1得到xy=1-(x2+y2),再由基本不等式和绝对值不等式得到-
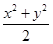 ≤-|xy|≤xy≤|xy|≤
≤-|xy|≤xy≤|xy|≤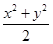 ,再将xy=1-(x2+y2)代入即可得到答案.
,再将xy=1-(x2+y2)代入即可得到答案.解:x2+xy+y2=1,
∴xy=1-(x2+y2),
又-
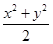 ≤-|xy|≤xy≤|xy|≤
≤-|xy|≤xy≤|xy|≤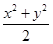 ,
,知-
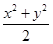 ≤1-(x2+y2)≤
≤1-(x2+y2)≤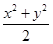 ,得出
,得出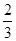 ≤x2+y2≤2.
≤x2+y2≤2.故选D

练习册系列答案
相关题目
 (1)当
(1)当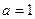 时,求不等式
时,求不等式 的解集;(2)如果不等式
的解集;(2)如果不等式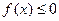 的解集为
的解集为 ,求
,求 的值。
的值。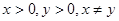 ,则下面四个数中最小的是
,则下面四个数中最小的是 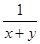
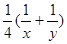


 ,且
,且 ,求证:
,求证:
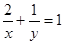 则
则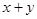 的最小值等于( )
的最小值等于( )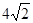
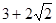
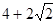
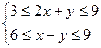 则z=x+2y的最小值为 .
则z=x+2y的最小值为 .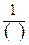 +
+ 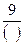 ”的两个括号内各填入
”的两个括号内各填入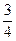
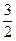
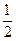
 满足:
满足: .
. ;(Ⅱ)求
;(Ⅱ)求 的最大值.( )
的最大值.( )