题目内容
已知直线x+2y-4=0与抛物线y2=4x相交于A、B两点,O是坐标原点,试在抛物线的弧
上求一点P,使△PAB面积最大.
 |
| AOB |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设出点P的坐标,求出P到直线l的距离的表达式,由不等式特点求面积最大时P的坐标,即可得出结论.
解答:
解:由题意
,化简为y2+8y-16=0,所以y1=-4+4
,y2=-4-4
,所以x1=12-8
,x2=12+8
,
设点P(t2,2t),因为P在抛物线的弧
上
所以-2-2
≤t≤-2+2
,
又P到直线l的距离为:d=
=
,t∈[-2-2
,-2+2
],
所以t=-2,即P(4,-4)时,P到直线l的距离最大,
即此时△PAB面积最大.
|
| 2 |
| 2 |
| 2 |
| 2 |
设点P(t2,2t),因为P在抛物线的弧
 |
| AOB |
所以-2-2
| 2 |
| 2 |
又P到直线l的距离为:d=
| |t2+4t-4| | ||
|
| |(t+2)2-8| | ||
|
| 2 |
| 2 |
所以t=-2,即P(4,-4)时,P到直线l的距离最大,
即此时△PAB面积最大.
点评:本题考查直线与抛物线的位置关系,考查点到直线距离公式的运用,适当设点的坐标,正确求出P到直线l的距离是关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若椭圆2kx2+ky2=1的一个焦点坐标是(0,4),则k的值为( )
A、
| ||
B、
| ||
| C、2 | ||
D、
|
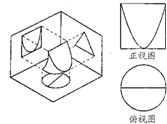 一个圆柱从顶部切掉两块,剩下部分几何体如图所示,此几何体的正视图和俯视图如图所示,其中正视图中的四边形是边长为2的正方形,则此几何体的侧视图的面积为( )
一个圆柱从顶部切掉两块,剩下部分几何体如图所示,此几何体的正视图和俯视图如图所示,其中正视图中的四边形是边长为2的正方形,则此几何体的侧视图的面积为( )