题目内容
已知二次函数y=a(a+1)x2-(2a+1)x+1,当a=1,2,…,n,…时,其对应的抛物线在x轴上截得的线段长依次为d1,d2,…,dn,…,则d1+d2+…+dn=
.
| n |
| n+1 |
| n |
| n+1 |
分析:当a=n时,y=n(n+1)x2-(2n+1)x+1,结合方程的根与系数关系可求dn,然后利用裂项求和方法即可求解.
解答:解:当a=n时,y=n(n+1)x2-(2n+1)x+1,
∴x1+x2=
,x1x2=
∴|x1-x2|=
=
=
-
∴d1+d2+…+dn=1-
+
-
+…+
-
=
故答案为:
∴x1+x2=
| 2n+1 |
| n(n+1) |
| 1 |
| n(n+1) |
∴|x1-x2|=
| (x1+x2)2-4x1x2 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴d1+d2+…+dn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| n |
| n+1 |
故答案为:
| n |
| n+1 |
点评:本题考查函数的二次函数的性质的运算,裂项求和公式的合理运用是求解的关键

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
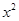 +bx+c,且a<0,a-b+c>0,则一定有(
)
+bx+c,且a<0,a-b+c>0,则一定有(
)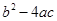 >0 B.
>0 B.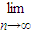 (d1+d2+…+dn)的值是( )
(d1+d2+…+dn)的值是( )