题目内容
设函数f(x)是定义在R上的增函数,且f(x)≠0,对于任意x1、x2∈R,都有f(x1+x2)=f(x1)·f(x2).
(1)求证:f(x1-x2)= ;
;
(2)若f(1)=2,解不等式f(3x)>4f(x).
(1)求证:f(x1-x2)=
 ;
;(2)若f(1)=2,解不等式f(3x)>4f(x).
(1)见解析
(2)不等式f(3x)>4f(x)的解集是{x|x>1}.
(2)不等式f(3x)>4f(x)的解集是{x|x>1}.
(1)∵f(x1)=f(x1-x2+x2)=f(x1-x2)·f(x2),
又f(x)≠0,
∴f(x1-x2)= .
.
(2)∵f(1)=2,∴2f(x)=f(1)·f(x)=f(1+x),
4f(x)=2·2f(x)=f(1)·f(1+x)=f(2+x).
那么f(3x)>4f(x)可化为f(3x)>f(2+x).
又∵函数f(x)是定义在R上的增函数,
由f(3x)>f(2+x),得3x>2+x,即x>1.
故不等式f(3x)>4f(x)的解集是{x|x>1}.
又f(x)≠0,
∴f(x1-x2)=
 .
.(2)∵f(1)=2,∴2f(x)=f(1)·f(x)=f(1+x),
4f(x)=2·2f(x)=f(1)·f(1+x)=f(2+x).
那么f(3x)>4f(x)可化为f(3x)>f(2+x).
又∵函数f(x)是定义在R上的增函数,
由f(3x)>f(2+x),得3x>2+x,即x>1.
故不等式f(3x)>4f(x)的解集是{x|x>1}.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ; ⑵
; ⑵  (a>0).
(a>0). ;
; )|x|;
)|x|; .
.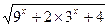 的值域.
的值域.
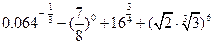
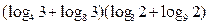
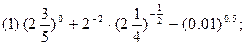 (2)
(2) 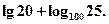
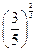 ,b=
,b=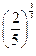 ,c=
,c=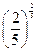 ,则a,b,c的大小关系是
,则a,b,c的大小关系是